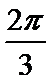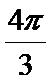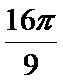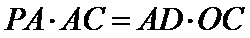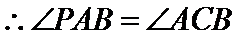- 真题试卷
- 模拟试卷
- 预测试卷
1.已知


正确答案
解析
由




考查方向
本题主要考查了集合的运算,为高考必考题,在近几年的各省高考题出现的频率较高,常与函数的定义域、解不等式等知识点交汇命题。
解题思路
先解不等式,再求交集。
易错点
解不等式过程中容易出错。
知识点
6.执行如图所示的程序框图,若输出的结果为2,则可输入的实数x值的个数为( )
正确答案
解析
由



考查方向
本题主要考查了程序框图与分段函数的综合应用问题,为高考必考题,在近几年的各省高考题出现的频率较高,常与数列求和、分段函数等知识点交汇命题。
解题思路
根据判断框条件直接计算对数的值。
易错点
对循环条件的判断失误导致出错。
知识点
7.已知数列5,6,1,-5,…,该数列的特点是从第二项起,每一项都等于它的前后两项之和,则这个数列的前16项之和
正确答案
解析
易知,该数列的前16项分别为5,6,1,-5,-6,-1,5,6,1,-5,-6,-1,5,6,1,-5,故
考查方向
解题思路
根据该数列的特点直接计算。
易错点
相关概念不熟悉导致出错。
知识点
9.已知函数




正确答案
解析
由










考查方向
解题思路
由


易错点
对条件

知识点
11. 已知双曲线
正确答案
解析
如下图所示,在三角形OF2B1中,由面积相等可得






考查方向
解题思路
根据题中条件建立等式,进而求出双曲线的离心率。
易错点
对于已知条件不知如何处理导致出错。
知识点
2.新定义运算:




正确答案
解析
由新概念可知

考查方向
本题主要考查了复数的运算,为高考必考题,在近几年的各省高考题出现的频率较高,常与复数的运算法则、几何意义等知识点交汇命题。
解题思路
通过对新概念的理解直接计算。
易错点
对新概念的不理解导致出错。
知识点
3.已知平面向量






正确答案
解析
由







考查方向
本题主要考查了平面向量的运算,为高考必考题,在近几年的各省高考题出现的频率较高,常与向量数量积的定义、性质等知识点交汇命题。
解题思路
直接运用公式求出向量

易错点
向量的运算率不熟悉导致出错。
知识点
4.甲乙两人有三个不同的学习小组A,B,C可以参加,若每人必须参加并且仅能参加一个学习小组,则两人参加同一个小组的概率为( )
正确答案
解析
甲乙两人每人必须参加并且仅能参加一个学习小组的基本事件总数为3×3=9个,两人参加同一小组包含3个基本事件,故其概率为
考查方向
本题主要考查了古典概型求概率,为高考必考题,在近几年的各省高考题出现的频率较高,常与古典概型概率计算公式等知识点交汇命题。
解题思路
找到基本事件空间后直接用古典概型的概率公式进行计算。
易错点
基本事件空间容易找错。
知识点
5. 下列判断错误的是( )
正确答案
解析
命题“若



考查方向
本题主要考查了命题与量词,为高考必考题,在近几年的各省高考题出现的频率较高,常与解不等式、点线面位置关系等知识点交汇命题。
解题思路
利用相关知识逐一进行判断。
易错点
相关知识点不熟悉导致出错。
知识点
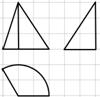
8.某几何体的三视图如图所示(图中网格的边长为1个单位),其中俯视图为扇形,则该几何体的体积为( )
正确答案
解析
易知,该几何体为底面半径为2高为3的圆锥的一部分,底面扇形的面积为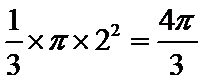
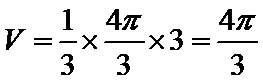
考查方向
解题思路
以三视图为载体考查空间线面位置关系的证明、求解其中一个视图的面积问题、求解几何体的表面积和体积问题等,解决此类问题的关键是能够对给出的三视图进行恰当的分析,从三视图中发现相应的位置关系与数量关系,然后在直观图中解决问.
易错点
不能由三视图还原为原图导致出错。
知识点
12. 定义在R上的函数





正确答案
解析
由











由图像可知该函数在一个周期内有2个零点,故函数


考查方向
解题思路
先利用


易错点
无法求出函数的周期导致出错。
知识点
10.已知三棱锥





正确答案
解析
设底面




考查方向
解题思路
先由题中条件求出球的半径,再由球的表面积公式求表面积。
易错点
无法找到球与椎体的联系。
知识点
15. 抛物线




正确答案
解析
试题分析:抛物线的焦点坐标为








考查方向
解题思路
根据题中所给条件直接计算。
易错点
对题所给条件不知如何应用导致本题没有思路。
知识点
13. 若


正确答案
解析
试题分析:画出可行域,如下图所示,作出直线
考查方向
解题思路
画出可行域,作出直线
易错点
不能准确画出可行域导致出错。
知识点
14. 在明朝程大位《算法统宗》中有这样的一首歌谣:“ 远看巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯”。 这首古诗描述的这个宝塔其古称浮屠,本题说它一共有7层,每层悬挂的红灯数是上一层的2倍,共有381盏灯,问塔顶有几盏灯? 你算出顶层有__________盏灯
正确答案
3
解析
试题分析:依据题意可知381÷(1+2+4+8+16+32+64)=381÷127=3(盏)。故此题答案为3。
考查方向
解题思路
根据题意直接计算。
易错点
题意不清楚导致出错。
知识点
16. 在




正确答案
解析
试题分析:由







考查方向
解题思路
由
易错点
对题所给条件不知如何应用导致本题没有思路。
知识点
已知等比数列








17.求

18.设数列




正确答案

解析
试题分析:本题属于数列知识的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
(1)设数列




考查方向
解题思路
(1)直接利用相关知识点求解;(2)利用裂项相消法求和.
易错点
相关知识点不熟容易处错。
正确答案

解析
试题分析:本题属于数列知识的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
由题意得:
考查方向
解题思路
(1)直接利用相关知识点求解;(2)利用裂项相消法求和.
易错点
相关知识点不熟容易处错。
在四棱锥












21.求证:

22.求点C到平面PBD的距离.
正确答案
见证明
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:
在正三角形ABC中,
在

所以

所以
在等腰直角三角形

所以

所以
又




考查方向
解题思路
(1)直接利用线面平行的判定定理进行证明;
(2)利用等体积法求点到面的距离.
易错点
相关定理不熟容易处错。
正确答案
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:
方法一:
∴
方法二:C到平面PBD距离等于A到PBD距离,即A到PM距离d,
∴
考查方向
解题思路
(1)直接利用线面平行的判定定理进行证明;
(2)利用等体积法求点到面的距离.
易错点
相关定理不熟容易处错。
十八届五中全会公报指出:努力促进人口均衡发展,坚持计划生育的基本国策,完善人口发展战略,全面实施一对夫妇可生育两个孩子的政策,提高生殖健康、妇幼保健、托幼等公共服务水平.为了解适龄公务员对放开生育二胎政策的态度,某部门随机调查了200位30到40岁的公务员,得到情况如下表:
19.是否有99%以上的把握认为“生二胎与性别有关”,并说明理由;
20.把以上频率当概率,若从社会上随机抽取甲、乙、丙3位30到40岁的男公务员,求这三人中至少有一人要生二胎的概率.
附:
正确答案
没有99%以上的把握认为“生二胎与性别有关”
解析
试题分析:本题属于概率与统计综合应用问题,属于简单题,只要掌握相关概率与统计的知识,即可解决本题,解析如下:
由于
=
故没有99%以上的把握认为“生二胎与性别有关”.
考查方向
解题思路
(1)直接利用K2分布公式求解;
(2)直接利用古典概型求概率.
易错点
相关知识点不熟容易出错。
正确答案

解析
试题分析:本题属于概率与统计综合应用问题,属于简单题,只要掌握相关概率与统计的知识,即可解决本题,解析如下:
题意可得,一名男公务员要生二胎的概率为

一名男公务员不生二胎的概率为

记事件A:这三人中至少有一人要生二胎
则
考查方向
解题思路
(1)直接利用K2分布公式求解;
(2)直接利用古典概型求概率.
易错点
相关知识点不熟容易出错。
如图,圆







23.求圆
24.过点




正确答案
解析
试题分析:本题属于圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:
设圆



∵ 


∴ 圆

考查方向
解题思路
(1)利用相关知识求圆方程;
(2)联立方程组,把角
易错点
对题中条件的处理容易出错。
正确答案
见证明
解析
试题分析:本题属于圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:
把



即点
(1)当

(2)当



联立方程

设直线



∴ 
考查方向
本题考查了求圆的方程、直线与椭圆位置关系等知识点。
解题思路
(1)利用相关知识求圆方程;
(2)联立方程组,把角
易错点
对题中条件的处理容易出错。
已知函数

25.若


26.函数



正确答案
解析
试题分析:本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:
当导函数


函数

所以实数

(也可以转化为恒成立问题。酌情给分。)
(还可以对方程
考查方向
解题思路
(1)直接利用单调性即可求参数范围;
(2)分离参数法求实数a的范围.
易错点
第二问对题中所给条件不知如何下手导致失分。
正确答案


解析
试题分析:本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:
由题意知,不等式

即







令 





(也可以构造函数
考查方向
本题考查了利用单调性求参数范围、不等式有解等知识点。
解题思路
(1)直接利用单调性即可求参数范围;
(2)分离参数法求实数a的范围.
易错点
第二问对题中所给条件不知如何下手导致失分。
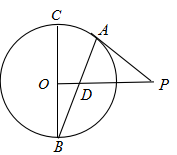
如图所示,直线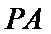
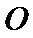
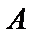
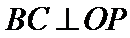

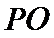
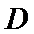
27.证明: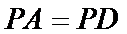
28.证明:
正确答案
见解析
解析
试题分析:本题属于圆的综合应用问题,属于简单题,只要掌握相关圆的知识,即可解决本题,解析如下:
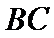
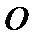
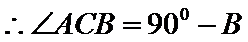
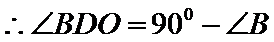
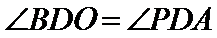
考查方向
解题思路
(1)利用切割线定理即可得证;
(2)利用三角形相似即可证明.
易错点
相关定理不熟悉导致本题失分。
正确答案
见证明.
解析
试题分析:本题属于圆的综合应用问题,属于简单题,只要掌握相关圆的知识,即可解决本题,解析如下:
连结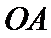
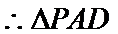

考查方向
解题思路
(1)利用切割线定理即可得证;
(2)利用三角形相似即可证明.
易错点
相关定理不熟悉导致本题失分。