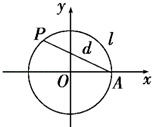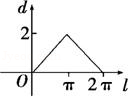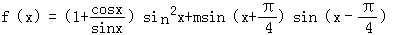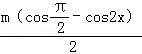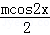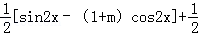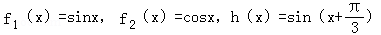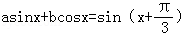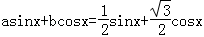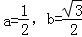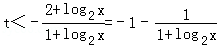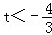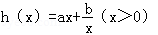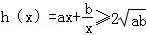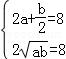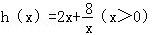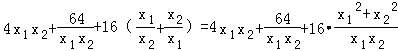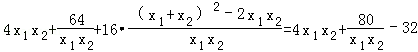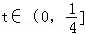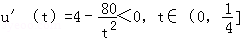- 真题试卷
- 模拟试卷
- 预测试卷
1．已知集合A={1，3，m}，B={3，4}，A∪B={1，2，3，4}，则m=_______
正确答案
2
解析
解析已在路上飞奔，马上就到！
知识点
5．已知
正确答案
3
解析
解析已在路上飞奔，马上就到！
知识点
6．对任意不等于1的正数a，函数f（x）=loga（x+3）的反函数的图象都经过点P，则点P的坐标是 _________
正确答案
（0，﹣2）
解析
解析已在路上飞奔，马上就到！
知识点
7．若函数y=sin2x+acos2x的图象关于直线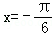
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．若数列{an}的前n项和Sn=n2﹣10n，（n∈N*），则an= _________ ．
正确答案
2n﹣11
解析
解析已在路上飞奔，马上就到！
知识点
9．函数f（x）=loga|x﹣b|（a＞0且a≠1）是偶函数，且在（0，+∞）上单调递减，则f（a﹣3）与f（b﹣2）的大小关系是 _________ ．
正确答案
f（a﹣3）＜f（b﹣2）
解析
解析已在路上飞奔，马上就到！
知识点
10．某种商品，若定价为p元，则每月可卖出n件，设定价上涨x成（一成即10%），卖出数量将减少
正确答案
（0，
解析
解析已在路上飞奔，马上就到！
知识点
2．不等式|2x﹣1|＜3的解集为_______
正确答案
{x|﹣1＜x＜2}
解析
解析已在路上飞奔，马上就到！
知识点
3．关于x的不等式
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．设f（x）为定义在R上的奇函数，当x≥0时，f（x）=2x+2x+b（b为常数），则f（﹣2）= _________ ．
正确答案
﹣1
解析
解析已在路上飞奔，马上就到！
知识点
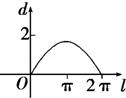
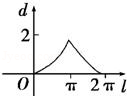
11．若sinx+|sinx|+k=0在（﹣π，π）内至少有两解，则实数k的取值范围是 _________ ．
正确答案
﹣2＜k≤0
解析
解析已在路上飞奔，马上就到！
知识点
12．无论m取何值，函数
正确答案
227
解析
解析已在路上飞奔，马上就到！
知识点
14．定义：关于x的两个不等式f（x）＜0和g（x）＜0的解集分别为（a，b）和
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．若关于x的方程
正确答案
（﹣
解析
解析已在路上飞奔，马上就到！
知识点
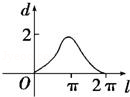
18．如图，设点A是单位圆上的一定点，动点P从A出发在圆上按逆时针方向转一周，点P所旋转过的弧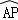
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．为了得到函数y=sin（2x﹣
A向左平移
B向右平移
C向左平移
D向右平移
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．若a、b、c∈R，a＞b，则下列不等式成立的是（ ）
A
Ba2＞b2
C
Da|c|＞b|c
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17．若x0是方程
A（
B（
C（
D（0，
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20．在△ABC中，角A，B，C的对边分别为
（1）求sinC的值；
（2）求△ABC的面积
正确答案
解：（1）∵A、B、C为△ABC的内角，
且
则sinA=
∴
∴
（2）由（1）知
又∵
∴在△ABC中，由正弦定理，得
∴
∴△ABC的面积
解析
解析已在路上飞奔，马上就到！
知识点
21．已知函数f（x）=（1+cotx）sin2x+msin（x+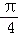
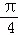
（1）当m=0时，求f（x）在区间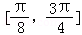
（2）当tana=2时，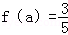
正确答案
解：（1）当m=0时，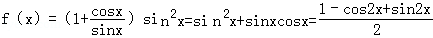
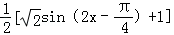
由已知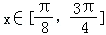
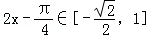
从而得：f（x）的值域为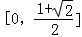
（2）因为
=sin2x+sinxcosx+
=
=
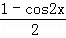
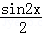
所以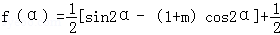
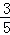
当tanα=2，得：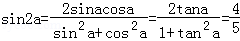
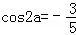
代入①式，解得m=﹣2．
解析
解析已在路上飞奔，马上就到！
知识点
22．已知函数
（1）当f（x）的定义域为
（2）试问对定义域内的任意x，f（2a﹣x）+f（x）的值是否为一个定值？若是，求出这个定值；若不是，说明理由；
（3）设函数g（x）=x2+|（x﹣a）f（x）|，若
正确答案
解：（1）函数
当 a+
于是﹣3≤﹣1+
即f（x）值域为[﹣3，﹣2]．
（2）∵f（2a﹣x）+f（x）=
对定义域内的所有x都成立，
∴对定义域内的任意x，f（2a﹣x）+f（x）的值是定值﹣2．
（3）解：当a=1时，g（x）=x2+|x|（x≠﹣1）
（ⅰ）当x≥0时，
则函数g（x）在[0，+∞）上单调递增，
g（x）min=g（0）=0
（ⅱ）当x≤0时，
则函数g（x）在（﹣∞，0]且x≠﹣1时单调递减，
g（x）min=g（0）=0
综合得：当x≠﹣1时，g（x）的最小值是0．
解析
解析已在路上飞奔，马上就到！
知识点
19．关于x的不等式
（1）求Q
（2）求a的取值范围．
正确答案
解：（1）∵等式
∴P=（﹣∞，﹣1）∪（a，+∞）
∵不等式log2（x2﹣1）≤1的解集为Q
∴Q：
∴
（2）由（1）求出的结果，若Q⊆P
有a≤1，且a是正数，
∴0＜a≤1
解析
解析已在路上飞奔，马上就到！
知识点
23．对于函数f1（x），f2（x），h（x），如果存在实数a，b使得h（x）=a•f1（x）+b•f2（x），那么称h（x）为f1（x），f2（x）的生成函数。
（1）下面给出两组函数，h（x）是否分别为f1（x），f2（x）的生成函数？并说明理由。
第一组：
第二组：f1（x）=x2﹣x，f2（x）=x2+x+1，h（x）=x2﹣x+1
（2）设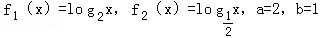
（3）设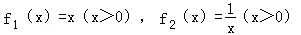
正确答案
解：（1）①设
即
取
所以h（x）是f1（x），f2（x）的生成函数
②设a（x2+x）+b（x2+x+1）=x2﹣x+1
即（a+b）x2+（a+b）x+b=x2﹣x+1
则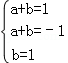
所以h（x）不是f1（x），f2（x）的生成函数
（2）
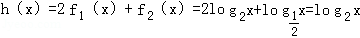
即log2（4x）+t•log2（2x）＜0
所以，（2+log2x）+t（1+log2x）＜0
因为x∈[2，4]，所以1+log2x∈[2，3]
则
函数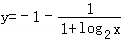
所以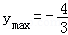
故
（3）由题意得，
则
故
解得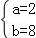
假设存在最大的常数m，使h（x1）h（x2）≥m恒成立
于是设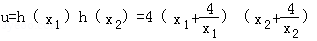
=
设t=x1x2，
则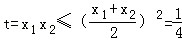
即
设
因为
所以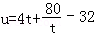
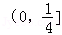
从而
故存在最大的常数m=289
解析
解析已在路上飞奔，马上就到！