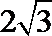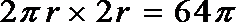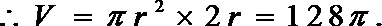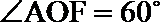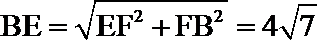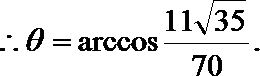- 真题试卷
- 模拟试卷
- 预测试卷
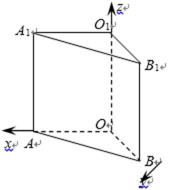
8.如图,直三棱柱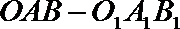
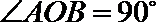
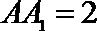
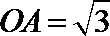
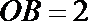
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.等差数列



正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
4.△ABC的内角A、B、C的对边分别为a、b、c,且asinA+csinC-

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 一次课程改革交流会上准备交流试点校的5篇论文和非试点校的3篇论文,排列次序可以是任意的,则最先和最后交流的论文不能来自同类校的概率是_____________
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设




正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
7.若实数x,y满足不等式组
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 定义某种运算




正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
12.给定两个长度为1的平面向量






正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
13.对函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.在平面直角坐标系





正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数






①
②
③
其中,具有性质
正确答案
① ③
解析
解析已在路上飞奔,马上就到!
知识点
16.设P是△ABC所在平面内的一点,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知a,b是实数,则“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知满足条件






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知向量

(1)求函数
(2)当


正确答案
(1)

由

(2)

所以
解析
解析已在路上飞奔,马上就到!
知识点
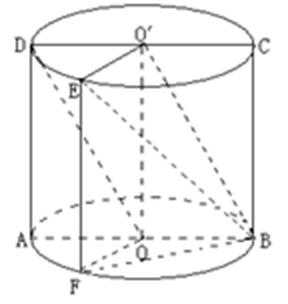
20.如下图,圆柱的轴截面
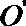
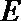
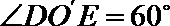
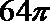
(1)求圆柱的体积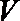
(2)求异面直线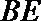
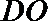
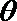
正确答案
(1)设圆柱的底面半径为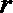
解得: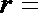
(2)连接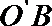
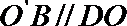
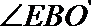
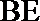
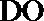
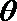
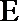
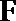
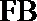
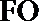
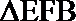
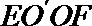
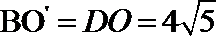
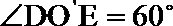
所以,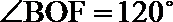
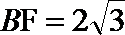
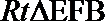
由余弦定理,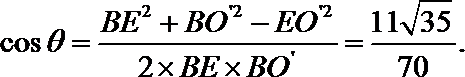
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)若

(2)若函数




正确答案
(1)
解得 
当

(2)由题意,




只有在

所以

解析
解析已在路上飞奔,马上就到!
知识点
22.在平面直角坐标系



(1)求到点


(2)过点







(3)已知点









正确答案
(1)由椭圆方程为







化简得点G的轨迹方程为
(2)由题意可知
故将

可得

(3) 假设存在实数
由已知得


椭圆C:
由①②解得
由①③解得
∴
故可得
解析
解析已在路上飞奔,马上就到!
知识点
23.已知数列{an}满足:
(1)求数列{an}的通项公式;
(2)当λ = 4时,若
(3)设Sn为数列{an}的前n项和.若对任意n∈N*,是否存在

正确答案
(1)当n=1时,a1=3.
当n≥2时,
因为
所以
①-②得
所以an=(2n+1)·λn-1(n≥2,n∈N*).
a1=3也适合上式,
所以an=(2n+1)·λn-1 (n∈N*).
(2)当λ=4时,
an=(2n+1)·4n-1
所以当
当

当
当

(3)Sn=3+5λ+7λ2+…+(2n+1)λn-1
当λ≠1时,Sn=3+5λ+7λ2+…+(2n+1)λn-1
λSn=3λ+5λ2+…+(2n-1)λn-1+(2n+1)λn
(1-λ)Sn=3+2(λ+λ2+λ3++…+λn-1)-(2n+1)λn=3+2×
假设对任意n∈N*,存在

但是当
当

矛盾,假设不成立
所以对任意n∈N*,不存在

解析
解析已在路上飞奔,马上就到!