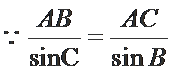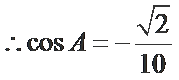- 真题试卷
- 模拟试卷
- 预测试卷
3.在平面直角坐标系

正确答案

解析


考查方向
解题思路
根据双曲线的性质以及
易错点
双曲线中
知识点
6.如图是一个算法的流程图,则输出
正确答案
9;
解析

则输出时
考查方向
解题思路
根据算法的程序流程逐项验证,直到循环终止输出结果。
易错点
循环终止的条件
知识点
5.函数
正确答案

解析



考查方向
解题思路
列出满足要求的不等式,利用不等式求解
易错点
列出所有满足要求的不等式
知识点
9.定义在区间


正确答案
7;
解析
画出函数图象草图,共7个交点.
考查方向
解题思路
画出两函数图像,找出交点个数。
易错点
图像画法,注意周期
知识点
10.如图,在平面直角坐标系





正确答案

解析
由题意得



由



则



考查方向
解题思路
设出各点坐标,根据向量数量积,列出方程,得到关于a,c的方程,求出e。
易错点
设点求解时正确建立方程关系。
知识点
1.已知集合

正确答案

解析
由交集的定义可得
考查方向
解题思路
在
易错点
范围与具体数字取交集的计算。
知识点
2.复数


正确答案
5;
解析
由复数乘法可得

考查方向
解题思路
根据复数的乘法运算化简结合复数定义求解。
易错点
复数中i2=-1.
知识点
4.已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是 .
正确答案

解析


考查方向
解题思路
根据方差公式求解
易错点
公式中要除以n。
知识点
7.将一个质地均匀的骰子(一种各个面上分别标有
正确答案

解析
将先后两次点数记为



考查方向
解题思路
列出所有基本事件空间以及发生事件的空间,利用比例解法求解。
易错点
列举事件的准确性。
知识点
8.已知





正确答案

解析
设公差为


解得


考查方向
解题思路
根据等差数列的通项以及求和列出方程组,求出基本量然后求特定项。
易错点
列方程求基本量致误
知识点
14.在锐角三角形
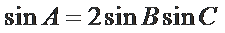
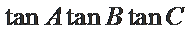
正确答案
8;
解析
由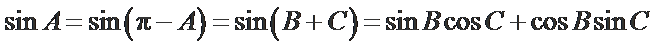
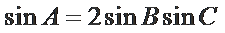
可得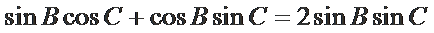
由三角形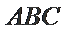
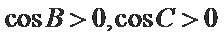
在(*)式两侧同时除以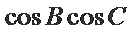
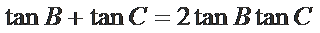
又
则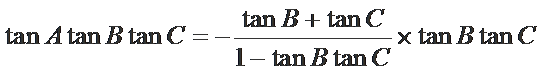
由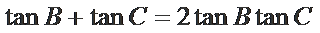
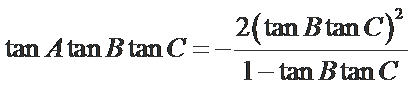
令
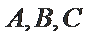
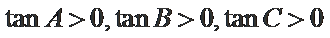
由(#)得
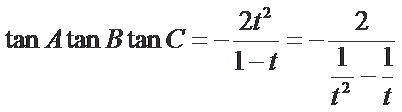

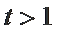
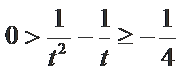

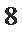
当且仅当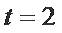


解得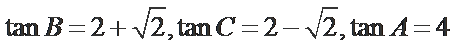
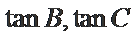
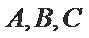
考查方向
解题思路
根据诱导公式、和差角公式化简,利用两边同除得到正切关系,应用正切公式的变形分析表示出
易错点
公式变形,函数关系转化,函数思想应用。
知识点
13.如图,在







正确答案

解析
令




则





则


由




因此
考查方向
解题思路
设出基向量,求出向量表达式,利用向量的关系通过转化求出数量积。
易错点
向量的线性转化运算。
知识点
12.已知实数


正确答案

解析
在平面直角坐标系中画出可行域如下

可以看出图中




图中




则
考查方向
解题思路
画出可行域,结合目标函数几何意义求最值。
易错点
注意最后要求距离的平方。
知识点
11.设


其中


正确答案

解析
由题意得

由


则
考查方向
解题思路
根据周期性求出a,然后代入应用周期性求值。
易错点
分段函数,周期性质
知识点
在
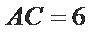

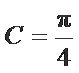
15.求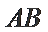
16. 求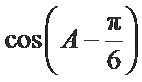
正确答案

解析
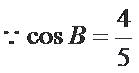

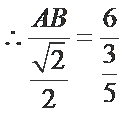
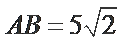
考查方向
解题思路
易错点
公式应用,公式变形。
正确答案

解析
又
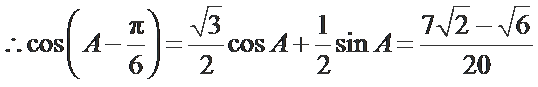
考查方向
解题思路
易错点
公式应用,公式变形。
现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥




19.若

20.若正四棱锥的侧棱长为

正确答案

解析





故仓库的容积为
考查方向
解题思路
易错点
列函数解析式,求导与分类讨论。
正确答案

解析
设
则






当


当


因此,当

即
考查方向
解题思路
易错点
列函数解析式,求导与分类讨论。
如图,在平面直角坐标系


及其上一点
21.设圆





22.设平行于





23.设点





正确答案
解析
因为



则圆

又圆



则



考查方向
解题思路
易错点
圆的方程、直线方程的求法及表示,位置关系中的几何表示。
正确答案

解析
由题意得





则


解得




考查方向
解题思路
易错点
圆的方程、直线方程的求法及表示,位置关系中的几何表示。
正确答案

解析





即

对于任意

此时


必然与圆交于


因此对于任意
综上
考查方向
解题思路
易错点
圆的方程、直线方程的求法及表示,位置关系中的几何表示。
记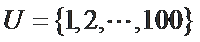
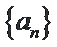

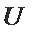
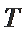
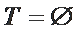
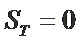
若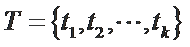
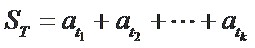
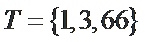
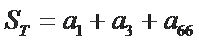
现设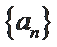

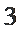
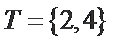
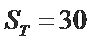
27.求数列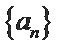
28.对任意正整数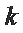
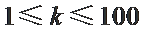
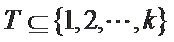
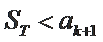
29.设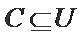
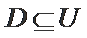
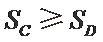
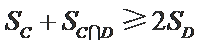
正确答案
解析
当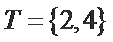
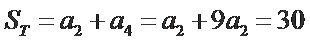
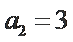
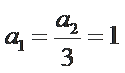
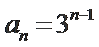
考查方向
解题思路
易错点
放缩,数列基本关系的转化,等比数列求和的应用
正确答案
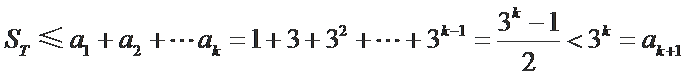
解析
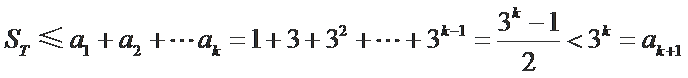
考查方向
解题思路
易错点
放缩,数列基本关系的转化,等比数列求和的应用
正确答案
设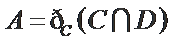
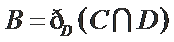
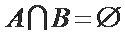
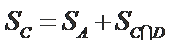
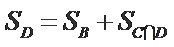
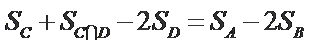
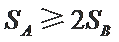
由条件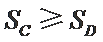
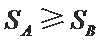
① 若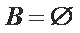
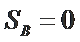
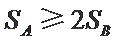
② 若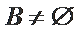
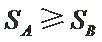
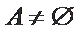
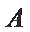
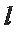
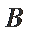
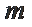
若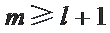
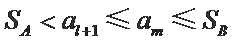
因为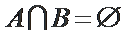
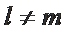
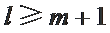
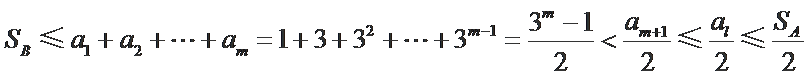
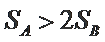
综上所述,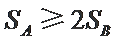
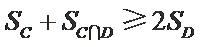
解析
设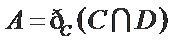
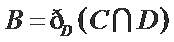
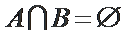
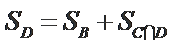
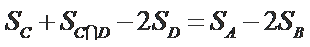
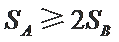
由条件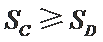
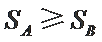
① 若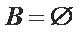
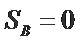
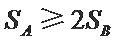
② 若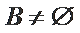
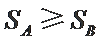
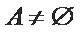
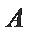
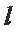
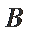
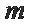
若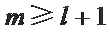
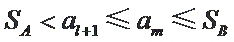
因为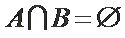
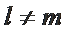
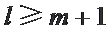
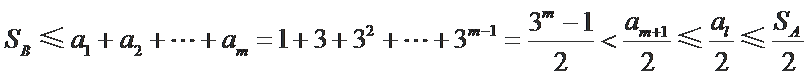
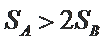
综上所述,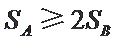
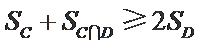
考查方向
解题思路
易错点
放缩,数列基本关系的转化,等比数列求和的应用
如图,在直三棱柱




且

17.直线

18.平面

正确答案



又





解析



又





考查方向
解题思路
易错点
判定定理的选用,线面关系的转化
正确答案



且



又

又

又







解析



且



又

又

又







考查方向
解题思路
易错点
判定定理的选用,线面关系的转化
已知函数
24.设


25. 若对于任意


26.若



正确答案
解析



则



考查方向
解题思路
易错点
基本不等式的应用,分类讨论思想,函数与方程思想
正确答案

解析
由题意得
令


此时

∵


因此实数

考查方向
解题思路
易错点
基本不等式的应用,分类讨论思想,函数与方程思想
正确答案

解析


由




而


因此







则




① 若








因此









则
② 若



可得
由
因此
因此


因此

考查方向
解题思路
易错点
基本不等式的应用,分类讨论思想,函数与方程思想
本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算步骤.
材料A.[选修4-1:几何证明选讲](回答30题)
如图,在





材料B.[选修4-2:矩阵与变换](回答31题)
已知矩阵


材料C.[选修4-4:坐标系与参数方程](回答32题)
在平面直角坐标系







材料D.[选修4-5:不等式选讲](回答33题)
设


回答下列问题
30.求证:
31.求矩阵
32.求线段
33.求证:
正确答案
由

由


则
由

由

因此
又

解析
由

由


则
由

由

因此
又

考查方向
解题思路
先由直角三角形斜边上中线性质






易错点
平面几何基本定理的应用
正确答案

解析


考查方向
解题思路
易错点
逆矩阵的转化运算
正确答案

解析
直线

椭圆

联立得


因此
考查方向
解题思路
易错点
参数方程与普通方程的互化。
正确答案


解析
由


考查方向
解题思路
利用含绝对值的不等式进行放缩证明
易错点
绝对值三角不等式的模式与应用。
如图,在平面直角坐标系


34.若直线


35.已知抛物线



①求证:线段

②求
正确答案

解析



即抛物线的焦点为

考查方向
解题思路
易错点
抛物线方程的形式,设而不求的思想。直线与抛物线的位置关系的运算程序。
正确答案
① 设点
则:

又

即
又




解析
① 设点
则:

又

即
又




② 






考查方向
解题思路
易错点
抛物线方程的形式,设而不求的思想。直线与抛物线的位置关系的运算程序。
回答下列问题。
36.求
37.设


正确答案
0
解析

考查方向
解题思路
根据组合数公式化简求值
易错点
组合数公式,错位相减求和,组合数性质的应用。
正确答案
对任意的
① 当


② 假设
即
当
左=

右边
而
因此
因此左边=右边,
因此
综合①②可得命题对任意
另解:因为
左边
又由

所以,左边
解析
对任意的
① 当


② 假设
即
当
左=

右边
而
因此
因此左边=右边,
因此
综合①②可得命题对任意
另解:因为
左边
又由

所以,左边
考查方向
解题思路
设置目的指向应用组合数性质解决问题,而组合数性质不仅有课本上的




易错点
组合数公式,错位相减求和,组合数性质的应用。