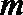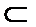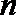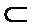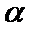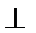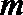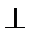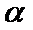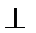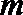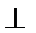- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在长方体ABCD—A1B1C1D1中,对角线B1D与平面A1BC1相交于点E,则点E为△A1BC1的( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.双曲线








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居众显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
①平均数
②标准差
③平均数

④平均数
⑤众数等于1且极差小于或等于1。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知如图所示的程序框图(未完成),设当箭头




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.直线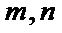
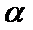
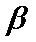
①若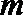
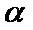
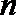

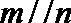
②若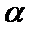
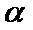
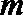
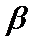
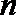
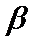
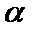
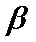
③若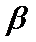
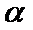
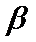
④若
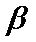
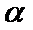
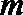

其中正确命题的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.假设你家订了一份早报,送报人可能在早上6:30—7:30之间把报纸送到你家,你父亲离开家去上班的时间在早上7:00—8:00之间,则你父亲离开家前能得到报纸的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.在抛物线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数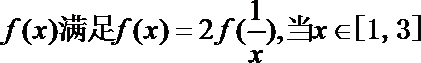
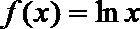
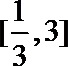
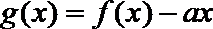
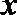
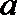
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设



正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
16.





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的外接球的表面积等于___________cm3.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知点


(1)求动点

(2)在







正确答案
(1)设动点

代入

(2)假设存在定点

设




所以
联立



要使得上式为定值,须


解析
解析已在路上飞奔,马上就到!
知识点
17. 已知





(1)求数列

(2)记





正确答案
由已知得
解析
解析已在路上飞奔,马上就到!
知识点
18. 节能灯的质量通过其正常使用时间衡量.使用时间越长,表明质量越好,若使用时间小于4千小时的产品为不合格品;使用时间在4千小时到6千小时的产品为合格品;使用时间大于6千小时的产品为优质品.某节能灯生产厂家为了解同一型号的某批次产品的质量情况,随机抽取了部分产品作为样本.得到试验结果的频率分布直方图如图所示.若以上述试验结果中使用时间落人各组的频率作为相应的概率.
(I)若该批次有产品2000件,试估计该批次的不合格品,合格品,优质品分别有多少件?
(II)已知该节能灯生产厂家对使用时间小于6千小时的





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数

(I)若函数


(II)


(III)求证:对于任意的


正确答案
(I)由题设,得



∵



(II)当





当




∴
当






(III)由(I)知函数

当





∴

解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24三题中任选一题做答。
22.选修 4-1:几何证明选讲
如图,在RtΔABC中,∠C=90°,BE平分∠ABC,交AC于点E,点D在AB上,DE⊥EB.
(Ⅰ)求证:AC是ΔBDE的外接圆的切线;
(Ⅱ)若AD=
23. 选修 4-4:坐标系与参数方程
在直角坐标系xOy中,圆C的参数方程
(Ⅰ)求圆C的极
(Ⅱ)直线



24. 选修 4-5:不等式选讲
已知函数
(Ⅰ)若


(Ⅱ)当



正确答案
22(I)证明:如图,取BD的中点O,连结OE。
∵BE平分

∵OB=OE,∴
∴
∵

∴AC是
(II)设圆O的半径为




∴OA=2OE,
∴

∴
23.(I)圆C的普通方程是

所以圆C的极坐标方程为
(II)设


设


由于

24.(I)
(II) 
当


当


当

所以不等式的解集为
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,在三棱锥A—BOC中,


(I)求证:
(II)在线段CB上是否存在一点F,使得在CO上任取一点G均有AG//平面DEF?若存在,试确定F的位置;若不存在,请说明理由.
正确答案
(I)证明:因为

因为OB=OC=1,BC=2,所以

因为AO与BO相交于点O,所以CO垂直于平面AOB。
(II)适合条件的点F在在,且F是BC的中点,证明如下:
取BC的中点F,连结DF、EF。
因为D是OB的中点,所以DF//OC,同理,EF//AC,所以平面DEF//平面AOC。
因为AG在平面AOC内,所以AG//平面DEF。
解析
解析已在路上飞奔,马上就到!