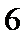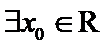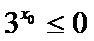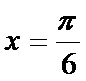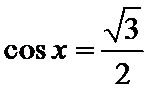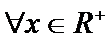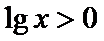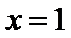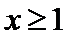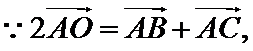- 真题试卷
- 模拟试卷
- 预测试卷
2.已知


正确答案
解析

考查方向
解题思路
根据题意,先求出a的值,然后用复数求模的方法求解
易错点
忽略
知识点
4. 某几何体的三视图如图所示,则该几何体的表面积为( )
正确答案
解析
如下图所示,由三视图可知几何体为正方体切去一个三棱锥得到的,正方体的棱长为1,切去的三棱锥为边长为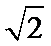
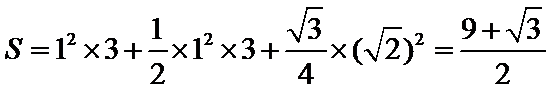
考查方向
解题思路
先根据三视图还原成空间几何体,再根据所给长度计算表面积
易错点
立体感不强,计算错误
知识点
5.已知实数



则使
正确答案
解析
因为



考查方向
解题思路
根据相关性质,结合选项直接选择正确答案
易错点
不理解题意,代入函数中“硬算”
知识点
8. 三棱锥P-ABC的三条侧棱两两垂直,三个侧面的面积分别是


正确答案
解析
因为三条侧棱两两垂直,所以可设



考查方向
解题思路
三棱锥的外接球实际上是它扩展为长方体的外接球,求长方体的对角线的长,就是球的直径,然后求球的体积
易错点
立体感不强;计算能力弱
知识点
1.已知全集



正确答案
解析
因为



考查方向
解题思路
根据题意,先确定集合A和B表示的x的范围,然后在求交集和补集
易错点
集合的基本概念理解不透彻
知识点
3.下列有关命题
正确答案
解析
A选项中,任何书的指数次幂都大于0,所以A错误,B中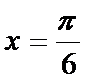
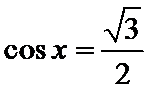
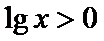
考查方向
解题思路
根据相关性质,逐一判断
易错点
对逻辑与命题理解不透彻
知识点
6. 阅读如图所示的程序框图,若输入

正确答案
解析
第1次,
第2次,
…………
第n次,
所以当输入 
考查方向
解题思路
根据程序框图的流程,计算运行n次的结果,根据输入的数值,判断n满足的条件,从而求出输出的值
易错点
选择语句判断错误
知识点
7.已知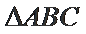
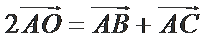
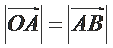
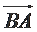
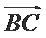
正确答案
解析
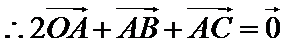
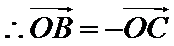
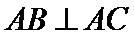
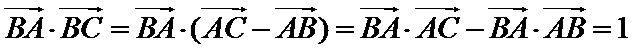
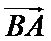
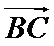
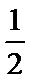
考查方向
解题思路
利用向量的运算法则将已知等式化简,对三角形的形状进行探究,利用运算法则展开求出投影,选出正确的选项
易错点
计算错误
知识点
9.已知双曲线




正确答案
解析
因为点在抛物线









考查方向
解题思路
根据题意先求出点P的坐标,代入上曲线方程,求出m的值,从而得到双曲线的渐近线方程
易错点
计算能力弱;分类讨论不全面
知识点
10. 数列




正确答案
解析
设数列

所以

考查方向
解题思路
先求出公差d,再根据等差数列的性质求出a11
易错点
对等差数列的性质运用错误
知识点
11. 已知角





正确答案
解析
根据函数的图象的相邻两条对称轴之间的距离等于






考查方向
解题思路
先求出周期w,再由条件求出
易错点
三角函数周期,同角三角函数转换错误。
知识点
12.如图,偶函数






正确答案
解析
由图象可知f(x)=0有三个根,0,
由图象可知,g(x)所对的每一个值都能有3个根,因此m=9,同理可得,n=9,所以选A.
考查方向
解题思路
结合函数图象把方程根的个数转化为函数图象的交点
个数,可分别求出m.n,进而得到答案
易错点
数型结合思想的相互转化错误
知识点
14.如图6,为了测量











则

正确答案
7
解析
在三角形ABC中,由余弦定理得,
在三角形ACD中,由余弦定理得,
因为A+C=180,所以


考查方向
解题思路
分别在三角形ABC和三角形ACD中使用余弦定理解出AC,列方程解出cosD,最后求出AC
易错点
计算错误,实际问题转化成数学模型的能力
知识点
13. 已知

正确答案
解析



考查方向
解题思路
先求出
易错点
计算错误,对公式定理掌握不好
知识点
15.若


正确答案
解析
由题意可知可行域如下图蓝色区域,所以可知
考查方向
解题思路
先作出不等式组所表示的平面区域,然后利用目标函数可取最值。
易错点
不等式的解法错误
知识点
16.对于实数a,b,定义运算“⊗”:a⊗b=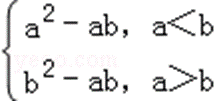
正确答案
解析
由题意可得函数的图像为下图,从图象上观察当关于X的方程为f(x)=m恰有三个互补相当的实数根时,函数的图形和直线y=m由三个不同的交点。再根据函数的极大值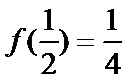
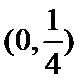
考查方向
解题思路
根据函数的解析式画出函数的图像,然后确定实数的取值范围。
易错点
计算错误,考虑情况不完全
知识点
已知数列



17.求数列
18.设



正确答案
见解析
解析








考查方向
解题思路
第1问,根据Sn和an的关系判断出数列为等比数列,根据等比数列通项公式求通项,第2问结合第1问得到的结论,得到Bn的通项,进而证明不等式
易错点
求数列通项公式错误
正确答案
见解析
解析




设




考查方向
解题思路
第1问,根据Sn和an的关系判断出数列为等比数列,根据等比数列通项公式求通项,第2问结合第1问得到的结论,得到Bn的通项,进而证明不等式
易错点
求数列通项公式错误
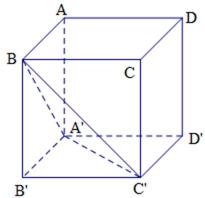
如图,在三棱柱








22.求

23.求证:

24.求三棱锥
正确答案
见解析
解析
证明:∵底面三边长













考查方向
解题思路
第一问由线面垂直证明线线垂直,第二问由线线平行证明线面平行,第三问根据三棱锥体积的计算公式,先求出三棱锥底面面积,再找到高,进而求解。
易错点
直线与平面的关系的判断与证明,逻辑错误
正确答案
见解析
解析
证明:设







∴






考查方向
解题思路
第一问由线面垂直证明线线垂直,第二问由线线平行证明线面平行,第三问根据三棱锥体积的计算公式,先求出三棱锥底面面积,再找到高,进而求解。
易错点
直线与平面的关系的判断与证明,逻辑错误
正确答案
见解析
解析
解:取


∵



又∵



∴

∵
∴
考查方向
解题思路
第一问由线面垂直证明线线垂直,第二问由线线平行证明线面平行,第三问根据三棱锥体积的计算公式,先求出三棱锥底面面积,再找到高,进而求解。
易错点
直线与平面的关系的判断与证明,逻辑错误
乐嘉是北京卫视 《我是演说家》的特约嘉宾,他的点评视角独特,语言犀利,给观众留下
19.从这60名男观众中按对乐嘉是否喜爱采取分层抽样,抽取一个容量为6的样本,问样本中喜爱与不喜爱的观众各有多少名?
20.根据以上列联表,问能否在犯错误的概率不超过0.025的前提下认为观众性别与喜爱乐嘉有关.(精确到0.001)
21.从19中的6
正确答案
见解析
解析
抽样比为
则样本中喜爱的观众有40×
考查方向
解题思路
第1问根据样本数据估计总体数据,第2问利用临界值表计算;第3问先把所有可能的情况列出来,然后用频率求概率
易错点
读取数据时错误,利用临界表公式计算错误
正确答案
见解析
解析
假设:观众性别与喜爱乐嘉无关,由已知数据可求得,
∴ 不能在犯错误的概率不超过0.025的前提下认为观众性别与喜爱乐嘉有关.
考查方向
解题思路
第1问根据样本数据估计总体数据,第2问利用临界值表计算;第3问先把所有可能的情况列出来,然后用频率求概率
易错点
读取数据时错误,利用临界表公式计算错误
正确答案
见解析
解析
记喜爱乐嘉的4名男性观众为a,b,c,d,不喜爱乐嘉的2名男性观众为1,2;则基本事件分别为:
(a,b),(a,c),(a,d),(a,1),(a,2),(b,c),(b,d),
(c,d),(c,1),(c,2),(d,1),(d,2),(1,2).
其中选到的两名观众都喜爱乐嘉的事件有6个,
故其概率为:P(A)=
考查方向
解题思路
第1问根据样本数据估计总体数据,第2问利用临界值表计算;第3问先把所有可能的情况列出来,然后用频率求概率
易错点
读取数据时错误,利用临界表公式计算错误
已知直线





25.若


26.若

正确答案
见解析
解析
解:设直线l与椭圆的两个交点坐标为


考查方向
解题思路
联立方程组,消去参数,利用基本不等式判断
易错点
计算错误;找不到最大值
正确答案
见解析
解析


由


当且仅当

又

所以,


考查方向
解题思路
联立方程组,消去参数,利用基本不等式判断
易错点
计算错误;找不到最大值
选修4—1;几何证明选讲
如图所示,圆











29.求证:△

30.如果

正确答案
见解析
解析

考查方向
解题思路
利用辅助线,做出相似三角形,根据相似求出相关线段的长
易错点
辅助线,三角形相似条件找不准
正确答案
见解析
解析



所以,
考查方向
解题思路
利用辅助线,做出相似三角形,根据相似求出相关线段的长
易错点
辅助线,三角形相似条件找不准
已知



27.求
28.若任意实数



正确答案
见解析
解析



没有递增区间;
考查方向
解题思路
先利用导数求函数的单调区间,第2问利用分类讨论思想,讨论参数的值。
易错点
求导数错误,参数的取值范围分类错误
正确答案
见解析
解析
由⑴可知,




令





而


考查方向
解题思路
先利用导数求函数的单调区间,第2问利用分类讨论思想,讨论参数的值。
易错点
求导数错误,参数的取值范围分类错误