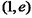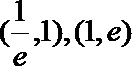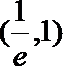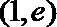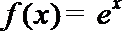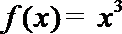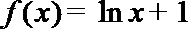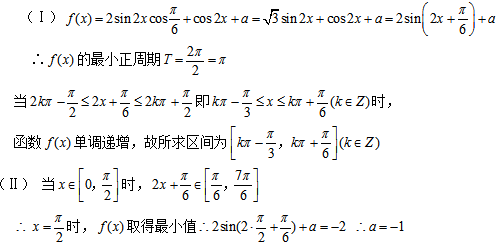- 真题试卷
- 模拟试卷
- 预测试卷
5. “


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 设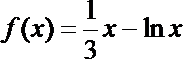

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 从双曲线










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 一个棱锥的三视图如图,则该棱锥的全面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在样本的频率分布直方图中,共有


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 在区间


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 在△ABC中,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点


正确答案
25
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知圆





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 对于函数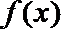
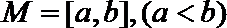
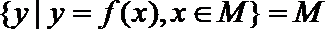
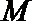
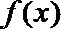
①
②
③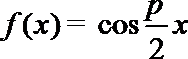
④
其中存在“稳定区间”的函数有______(填上所有正确的序号)
正确答案
②③
解析
解析已在路上飞奔,马上就到!
知识点
14.已知x,y满足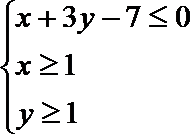
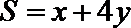
正确答案
9
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数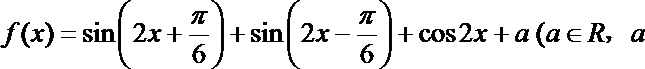
(Ⅰ)求函数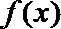
(Ⅱ)当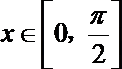
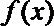
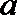
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知所有项均为正数的数列{an}中,



(Ⅰ)求证数列
(Ⅱ)设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 联合国准备举办一次有关全球气候变化的会议,分组研讨时某组有6名代表参加,A、B
两名代表来自亚洲,C、D两名代表来自北美洲,E、F两名代表来自非洲,小组讨论后将随
机选出两名代表发言。
(Ⅰ)代表A被选中的概率是多少?
(Ⅱ)选出的两名代表“恰有1名来自北美洲或2名都来自非洲”的概率是多少?
正确答案
(Ⅰ)从这6名代表中随机选出2名,共有15种不同的选法,分别为
(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),
(B,F),(C,D), (C,E),(C,F),(D,E),(D,F),(E,F).
其中代表A被选中的选法有(A,B),(A,C),(A,D),(A,E),(A,F)共5种,
则代表A被选中的概率为
(Ⅱ)随机选出的2名代表“恰有1名来自北美洲或2名都来自非洲”的结果有9种,
分别是(A,C),(A,D),(B,C),(B,D),(C,E),(C,F),(D,E),
(D,F),(E,F).
“恰有1名来自北美洲或2名都来自非洲”这一事件的概率为
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图所示,在棱长为2的正方体





(Ⅰ)求证:

(Ⅱ)求证:
(Ⅲ)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22. 已知椭圆C过点
且|PF|、|MF|、|QF|成等差数列。
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)求证:线段PQ的垂直平分线经过一个定点A;
(Ⅲ)在(Ⅱ)条件下,点A关于原点O的对称点是B,求|PB|的最小值及相应点P的坐标。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数
(Ⅰ)求函数
(Ⅱ)若




正确答案
解析
解析已在路上飞奔,马上就到!