- 真题试卷
- 模拟试卷
- 预测试卷
2.设集合 A={y∈R|y=3x,x∈R},B={-1,0,1},则下列结论正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设等比数列{an}的公比为q,前n项和为Sn,则“|q|=1”是S4=2S2的( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知有结论若a、b∈R+ ,a≠b,x,y∈(0,+∞) 则,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数f(x)在R上可导,f(x)的导函数为f′(x) ,则下列选项中正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数f(x)=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.5位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品,已知5位同学之间共进行了8次交换,则收到4份纪念品的同学人数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.执行如图所示的算法流程图,则输出的S的值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.定义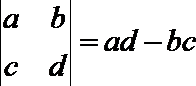
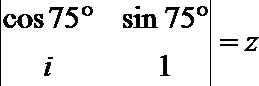
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若点P(-1,2,-3)关于x轴的对称点为Q,则点P,Q之间的距离为___________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知四面体P-ABC的外接球的球心O在AB上,且PO⊥平面ABC,2AC=AB,若四面体P-ABC的体积为,则该球的表面积为___________。
正确答案
12π
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数f(x)=asinx+bcosx(x∈R,ab≠0),给出下列命题:
①存在a,b使f(x)是奇函数;
②若对任意x∈R,存在x1x2,使f(x1)≤f(x)≤f(x2)成立,则的最小值为;
③过点(a,b)作直线l,则直线l与函数f(x)= asinx+bcosx(x∈R,ab≠0)的图像必有交点;
④若对任意x∈R,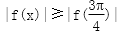
⑤若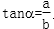
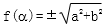
其中正确的是___________(写出所有正确命题的序号)
正确答案
②③④⑤
解析
解析已在路上飞奔,马上就到!
知识点
12.若数列{an}(公差为d)为等差数列,则数列{an}是首项为a1,公差为的等差数列;类似的,数列{bn}(bn>0,公比q>0)为等比数列,则___________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知正方形ABCD的边长为1,点E是AB边上的动点,则


正确答案
1;1
解析
解析已在路上飞奔,马上就到!
知识点
16.在△ABC中,角A,B,C所对的边分别为a,b,c,已知a=2,b=
(I)求c的值及△ABC的面积S;
(II)求的sin(2A+C)值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.在数列{an}中a1=1,3anan-1+an-an-1=0(n≥2).数列{bn}满足bn=an·an+1,Tn为数列{bn}的前n项和。
(1) 证明数列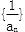
(2)若对任意的n∈N*,不等式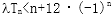
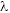
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(I) 求函数f(x)的极值;
(II) 若函数f(x)的图像与函数g(x)=1的图像在区间(0,e2]上有公共点,求实数a的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.曲线C:x|x|+y|y|=1
(I) 直线x+y-b=0与曲线C交于A,B两点用b表示|AB|的长;
(II) 分别过A,B作直线x+y=0的垂线,垂足分别为C,D,求四边形ABCD面积的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.为加强中学生实践、创新能力和团队精神的培养,促进教育教学改革,合肥市教育局举办了全市中学生创新知识竞赛,合肥一中举行选拔赛,共有200名学生参加,为了解成绩情况,从中抽取50名学生的成绩(得分均为整数,满分为100分)进行统计,请你根据尚未完成的频率分布表,解答下列问题;
(I) 求出a,b,c,d,e的值,并作出频率分布直方图;
(II)若成绩在85.5~95.5的学生均获二等奖,问合肥一中所有参赛学生中获得二等奖的学生约为多少人?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
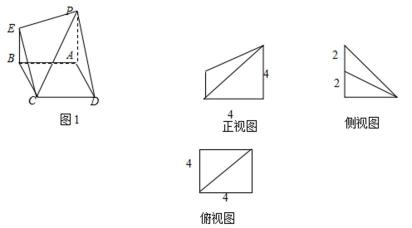
18.图1是一几何体的直观图,右图是该几何体的三视图。
(I) 若F为PD的中点,求证AF⊥平面PCD;
(II) 求几何体BCE—APD的体积;
(III) 若PB和AE交于G点,求四棱锥G—ABCD的体积。
正确答案
解析
解析已在路上飞奔,马上就到!