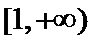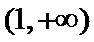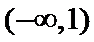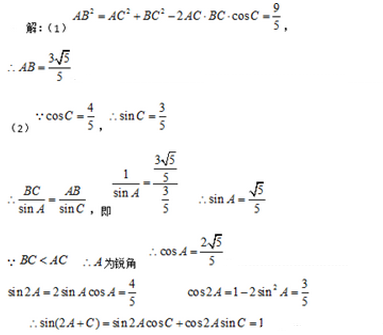- 真题试卷
- 模拟试卷
- 预测试卷
3.设集合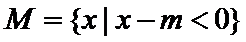
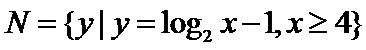
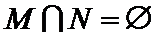
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.等差数列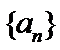
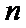
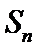
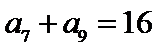
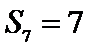
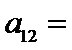
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设动点






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若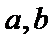
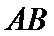
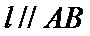
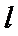

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.为了解某校高中学生的近视眼发病率,在该校学生分层抽样调查,高一、高二、高三分别有学生800名,600名,500名。若高三学生共抽取25名,则高一年级每位学生被抽到的概率为____________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.读下图,若

正确答案
120
解析
解析已在路上飞奔,马上就到!
知识点
13.已知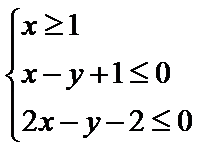
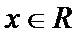
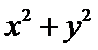
正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
9.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知



正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
14.设点






正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
15.我们称离心率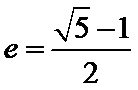
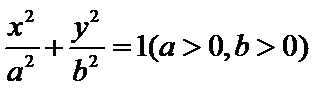
①长半轴长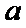
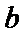
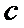
②一个长轴顶点与其不同侧的焦点以及一个短轴顶点构成直角三角形.
③以两条通经的4个端点为顶点的四边形为正方形.
④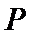
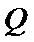
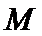
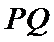
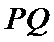
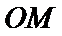
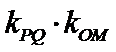
其中正确命题的序号为____________。
正确答案
①②③④
解析
解析已在路上飞奔,马上就到!
知识点
16.在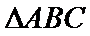
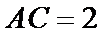
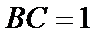
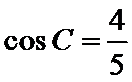
(1)求边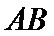
(2)求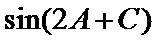
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某班10名同学在一次测试中英语和法语成绩(单位:分)如下图所示:
(1)比较哪门课程的平均成绩更高;
(2)计算10名同学法语成绩的样本方差;
(3)计算两门功课成
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在三棱锥




(1)求证:
(2)求二面角
(3)求点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设




(1)求双曲线的方程;
(2)已知直线







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知等差数列




(1)求数列


(2)若数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设函数
(1)若对定义域内任意


(2)若函数

(3)若


正确答案
解析
解析已在路上飞奔,马上就到!