- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合A={-3,-1,1,2},B={-2,0,1,2},则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.某市修建经济适用房,已知A、B、C三个社区分别有低收入家庭400户、300户、200户,若首批经济适用房有90套住房用于解决住房紧张问题,采用分层抽样的方法决定各社区户数,则应从A社区中抽取低收入家庭的户数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.“sin2θ<0”是“tanθ<0”的( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设f (x)是(-∞,+∞)上的奇函数,f (x+2)=-f (x),当0≤x≤1时有f (x)=2x,则f (2015)=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设x、y满足约束条件
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.某程序框图如图所示,该程序运行后输出S的值是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.一个几何体的三视图如图所示,已知正(主)视图是底边长为1的平行四边形,侧(左)视图是一个长为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.定义运算M:xy=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设F为抛物线y2=5x的焦点,P是抛物线上x轴上方的一点,若|PF|=3,则直线PF的斜率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若函数f (x)=ex+4x-kx在区间
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知A为射线x+y=0(x<0)上的动点,B为x轴正半轴上的动点,若直线AB与圆x2+y2=1相切,则|AB|的最小值为__________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在1,3,5,7中任取两个不同的数,则这两个数的和为8的概率为__________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在△ABC中,A=45°,AB=2,BC=3,则AC=__________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知数列{an}中,a1=3,a2=5,且{an-1}是等比数列。
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=nan,求数列{bn}的前n项和Tn。
正确答案
解:
(Ⅰ)∵{an-1}是等比数列且a1-1=2,a2-1=4,
∴an-1=2•2n-1=2n,∴an=2n+
(Ⅱ)bn=nan=n•2n+n
故Tn=b1+b2+b3+…+bn=(2+2×22+3×23+…+n•2n)+(1+2+3+…+n)[]
令T=2+2×22+3×23+…+n•2n则
2T=22+2×22+3×24+…+n•2n+1
两式相减得-T=2+22+23+…+2n-n•2n+1=
∴T=2(1-2n)+n7`2n+1=2+(n-1)•2n+1
∵1+2+3+…+n=
解析
解析已在路上飞奔,马上就到!
知识点
19.四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N分别是AB、SC、AD的中点。
(Ⅰ)求证:MN∥平面SAD;
(Ⅱ)求证:平面SOB⊥平面SCM。
正确答案
解:
(Ⅰ)如图,取SD的中点R,连结AR、RN,
则RN∥CD,且
∴RN∥AM,且RN=AM
∴四边形AMNR是平行四边形
∴MN∥AR,由AR平面SAD,MN
∴MN∥平面SAD
(Ⅱ)如图,设OB∩CM=H,由SO ⊥AD,面SAD ⊥面ABCD
∴SO⊥平面ABCD,∴CM⊥SO
易得
则∠BMH+∠ABO=∠BMH+∠BCM=90°
∴CM⊥OB
∴CM ⊥平面SOB
∵CM平面SCM
∴平面SOB ⊥平面SCM
解析
解析已在路上飞奔,马上就到!
知识点
20.已知一椭圆E的中心在坐标原点,左右焦点在x轴上,若其左焦点F1(-c,0)(c>0)到圆C:(x-2)2+(y-4)2=1上任意一点距离的最小值为4,且过椭圆右焦点F2(c,0)与上顶点的直线与圆
(Ⅰ)求椭圆E的方程;
(Ⅱ)若直线l:y=-x+m与椭圆E交于A、B两点,当以AB为直径的圆与y轴相切时,求△F1AB的面积。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分,作答时标出所选题目的题号。
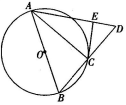
22.几何证明选讲 如图,AB是圆O的直径,点C在圆O上,延长BC到D,使BC=CD,过点C作圆O的切线交AD于E。
(Ⅰ)求证:CE⊥AD;
(Ⅱ)若AB=2,ED=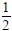
23.坐标系与参数方程在直角坐标系xOy中,圆C的参数方程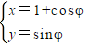
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)直线l的极坐标方程是ρ(sinθ+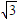
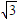
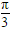
24. 不等式选讲 已知函数f (x)=|x-1|.
(Ⅰ)解不等式f (x)+f (x+4)≥8;
(Ⅱ)若|a|<1,|b|<1,且a≠0,求证: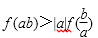
正确答案
22.
23.
24.
解析
解析已在路上飞奔,马上就到!
知识点
18.某市地铁即将于2015年6月开始运营,为此召开了一个价格听证会,拟定价格后又进行了一次调查,随机抽查了50人,他们的收入与态度如下:
(Ⅰ)若以区间的中点为该区间内的人均月收入,求参与调查的人员中“赞成定价者”与“认为价格偏高者”的月平均收入的差距是多少(结果保留2位小数);
(Ⅱ)由以上统计数据填下面2乘2列联表并分析是否有99%的把认为“月收入以5500元为分届点对地铁定价的态度有差异”。
参考数据
正确答案
解:
(Ⅰ)“赞成定价者”的月平均收入为
“认为价格偏高者”的月平均收入为:
“赞成定价者”与“认为价格偏高者”的月平均收入的差距是:
x1-x2=50.56-38.75=11.81(百元)
∴没有99%的把握认为月收放以5500为分届点对地铁定价的态度有差异。
解析
解析已在路上飞奔,马上就到!
知识点
21.定义在(0,+∞)上的三个函数f (x),g(x),h(x),已知f (x)=lnx,

(Ⅰ)求a的值及h(x)的单调区间;
(Ⅱ)求证:当

正确答案
解:
解析
解析已在路上飞奔,马上就到!