- 真题试卷
- 模拟试卷
- 预测试卷
1.已知全集U=R,集合A={x|1<x≤3},B={x|x>2},则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.如图给出的是计算
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知A(3,0),B(0,4),若圆M:



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知实数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知点P在以




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知复数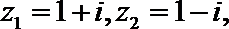
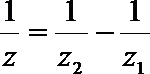
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知定义在R上的函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.将函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知命题



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数



正确答案
9
解析
解析已在路上飞奔,马上就到!
知识点
11.角




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.给出下列四个命题:
① 函数

② 若

③ 存在唯一的实数

④ 已知






其中正确命题的序号是________。
正确答案
②③
解析
解析已在路上飞奔,马上就到!
知识点
14.在





正确答案
-4
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆C: 


(1)求椭圆C的方程。
(2)已知过点T(0,2)的直线




正确答案
解:(1)

设
由于



当


故所求椭圆方程为
(2)由已知,以AB为直径的圆与X轴有公共点,
设
直线






所以,所求直线

解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数

(1)求函数
(2)已知△ABC中角 A.B.C所对的边分别是



正确答案
解:(1)由已知函数
又当

所以
(2)
又由于
解析
解析已在路上飞奔,马上就到!
知识点
18.已知




(1)求数列{
(2)若数列





正确答案
解: (1)
(2)



所以
解析
解析已在路上飞奔,马上就到!
知识点
17.在某高校自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级. 某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有10人.
(1)求该考场考生中“阅读与表达”科目中成绩为A的人数;
(2)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分,求该考场考生“数学与逻辑”科目的平均分;
(3)已知参加本考场测试的考生中,恰有两人的两科成绩均为A. 在至少一科成绩为A的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为A的概率。
正确答案
解: (1)因为“数学与逻辑”科目中成绩等级为B的考生有10人,
所以该考场有
所以该考场考生中“阅读与表达”科目中成绩等级为A的人数为

(2)该考场考生“数学与逻辑”科目的平均分为
(3)因为两科考试中,共有6人得分等级为A,又恰有两人的两科成绩等级均为A,
所以还有2人只有一个科目得分为A,
设这四人为甲,乙,丙,丁,其中甲,乙是两科成绩都是A的同学
则在至少一科成绩等级为A的考生中,随机抽取两人进行访谈,基本事件空间为


设“随机抽取两人进行访谈,这两人的两科成绩等级均为A”为事件B
所以事件B中包含的基本事件有1个,则
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在四棱锥








(1)求证:
(2)在线段



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(1)求实数

(2)若






正确答案
解:(1)由已知

由


所以函数

(2)由已知
由(1)知函数

由于



所以实数
解析
解析已在路上飞奔,马上就到!