- 真题试卷
- 模拟试卷
- 预测试卷
1.设复数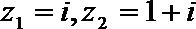
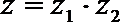
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.如图,矩形长为6,宽为2,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为96颗,以此实验数据为依据可以估算出椭圆的面积约为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若某空间几何体的三视图如图所示,则该几何体的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.圆

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在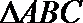
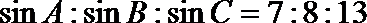
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.关于直线

①若





②若



③若




④若
其中假命题的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.“


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.中心在原点,焦点在
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在如图的所示的茎叶图中,甲、乙两组数据的中位数分别为( ),( )。
正确答案
45, 46
解析
解析已在路上飞奔,马上就到!
知识点
14.对任意非零实数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.我们可以利用数列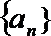
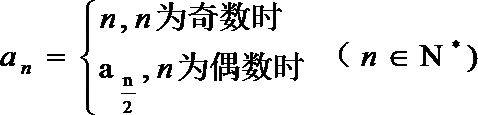
正确答案
640
解析
解析已在路上飞奔,马上就到!
知识点
15.不等式组
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
17.已知数列





(1)求

(2)若



正确答案
解:(1)由已知 
解得
设等差数列的公差为

∴
故
综上,
(2)∵
∴
=(
=
即 
解析
解析已在路上飞奔,马上就到!
知识点
19.为了了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm之间的概率;
(3)从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率。
正确答案
(1)由已知,抽取的学生人数为700
又由统计图知,男生抽取了40人,女生抽取了30人,故男生抽取的比例为
故估计男生的人数为
(2)由统计图知,男生身高在170~185的人数为14+13+4=31(人)
女生身高在170~185的人数为3+1=4(人)
∴ 估计该校学生身高在170~185cm的概率为
(3)样本中身高在180~190cm之间的男生共有6人,其中4人身高在180~185cm,分别设这四人为1,2,3,4;还有两人身高在185~190cm, 分别设这两人为A.B。
则从此6人中抽取两人,有(1,2)(1,3)(1,4)(1,A)(1,B)(2,3)(2,4)(2,A)(2,B)(3,4)(3,A)(3,B)(4,A)(4,B)(A,B)
共15种可能结果,每种结果是等可能的,所以试验中包含15个基本事件。
设事件T:“至少有1人身高在185~190cm之间”
则它包含(1,A)(1,B)(2,A)(2,B)(3,A)(3,B)(4,A)(4,B)(A,B)共9种基本事件, ∴
所以至少有一人身高在185~190cm之间的概率为
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数
(1)求函数

(2)在给定的坐标系中,画出函数
正确答案
解:(1)∵
=
=
故当
∴函数

(2) 略
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,DE垂直平分PC,且分别交AC、PC于D、E两点,又PB=BC,PA=AB。
(Ⅰ)求证:PC⊥平面BDE;
(Ⅱ)若点Q是线段PA上任一点,求证:BD⊥DQ;


正确答案
(Ⅰ)证明:由等腰三角形PBC,得BE⊥PC
又DE垂直平分PC,∴DE⊥PC
且
∴ PC⊥平面BDE
(Ⅱ)由(Ⅰ)知PC⊥平面BDE ∴ PC⊥BD
∵ PA⊥底面ABC ,
∴ PA⊥BD,又
∴ BD⊥平面PAC,
又点Q是线段PA上任一点,故
∴ BD⊥DQ
(Ⅲ)解:存在这样的点Q,使得PC//平面BDQ
不妨令PA=AB=1,则有PB=BC=
由

所以点Q在线段PA的

又
从而PC//平面BDQ .
解析
解析已在路上飞奔,马上就到!
知识点
21.椭圆C:

(1)求椭圆C的方程;
(2)设直线



正确答案
解(1)依题意,可知

∴
故所求的椭圆方程为
(2)联立方程

则
解得
设
则
① 若

∴
可解得
经检验
所以直线
② 若


联立方程
解得
Ⅰ.若A(


Ⅱ.若B(-

所以
综上可知 ,

另解:② 若


联立方程
则点(



解析
解析已在路上飞奔,马上就到!
知识点
22.已知直线




求(Ⅰ)求直线
(Ⅱ)设

正确答案
(Ⅱ)方法一:
由
得
设
当



于是,


故
要使
∴ a的取值范围为
方法二:由(Ⅰ)知,
∴






故


故

要使解得
只需
(ii)若




故不可能
综上所述,
解析
解析已在路上飞奔,马上就到!