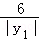- 真题试卷
- 模拟试卷
- 预测试卷
2. 函数f(x)=sin(x+
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 已知A,B,C三点不重合,则“
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线y=f(x),一种是平均价格曲线y=g(x)(如f(2)=3表示开始交易后第2小时的即时价格为3元;g(2)=4表示开始交易后两个小时内所有成交股票的平均价格为4元).下面所给出的四个图象中,实线表示y=f(x),虚线表示y=g(x),其中可能正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 已知集合A={x|x>0},B={x|﹣1≤x≤2},则A∪ B=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 若a>0且a≠1,函数y=ax﹣3+1的反函数图象一定过点A,则A的坐标是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 设a,b为两条直线,α,β为两个平面,下列四个命题中,正确的命题是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 若实数x,y满足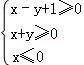
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 若曲线y2=2px(p>0)上有且只有一个点到其焦点的距离为1,则p的值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 
正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
9. 函数f(x)=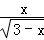
正确答案
(﹣∞,3)
解析
解析已在路上飞奔,马上就到!
知识点
11. 在△ABC中,AC=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知等差数列{an}的首项a1及公差d都是整数,前n项和为Sn(n∈N*).若a1>1,a4>3,S3≤9,则通项公式an=________.
正确答案
n+1
解析
解析已在路上飞奔,马上就到!
知识点
14. 定义一个对应法则f:P(m,n)→P′(

正确答案
(2,2),
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知圆C:x2+y2+6x﹣8y=0内有一点A(﹣5,0),直线l过点A交圆C于P,Q两点,若A为PQ中点,则|PQ|=2
正确答案

解析
解析已在路上飞奔,马上就到!
知识点
16.在一次百米比赛中,甲,乙等6名同学采用随机抽签的方式决定各自的跑道,跑道编号为1至6,每人一条跑道
(Ⅰ)求甲在1或2跑道且乙不在5或6跑道的概率;
(Ⅱ)求甲乙之间恰好间隔两人的概率.
正确答案
没有限制条件的种数为A66=720种,
(Ⅰ)先安排甲,再安排乙,剩下的全排,故有C21C31A44=144种,
根据概率公式,故甲在1或2跑道且乙不在5或6跑道的概率P=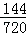
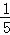
(Ⅱ)先选2人放在甲乙之间,并捆绑在一起,看作一个复合元素,再和剩下的2人全排,故有A42A22A33=144种,
根据概率公式,故甲乙之间恰好间隔两人的概率P=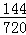
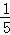
解析
解析已在路上飞奔,马上就到!
知识点
18.数列{an}的前n项和记为Sn,a1=1,an+1=2Sn+1(n≥1)
(Ⅰ)求{an}的通项公式;
(Ⅱ)等差数列{bn}的各项为正,其前n项和为Tn,且T3=15,又a1+b1,a2+b2,a3+b3成等比数列,求Tn.
(Ⅲ)设c∈,在(2)的条件下,设g(n)=Tn﹣cn,求g(n)的最小值.
正确答案
(Ⅰ)由an+1=2Sn+1可得an=2Sn﹣1+1(n≥2),
两式相减得an+1﹣an=2an,an+1=3an(n≥2)
又a2=2S1+1=3,∴a2=3a1
故{an}是首项为1,公比为3的等比数列.
∴
(Ⅱ)设{bn}的公差为d,
由T3=15得,可得b1+b2+b3=15,可得b2=5,
故可设b1=5﹣d,b3=5+d,
又a1=1,a2=3,a3=9,
由题意可得(5﹣d+1)(5+d+9)=(5+3)2
解得d1=2,d2=﹣10,
∵等差数列{bn}的各项为正,∴d>0,
∴d=2,b1=3,
∴
(Ⅲ)由已知得:g(n)=n2+2n﹣cn,对称轴
c∈,∴
①若c∈,此时g(n)最小值为g(2)=8﹣2c.
解析
解析已在路上飞奔,马上就到!
知识点
19.设椭圆
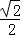

(Ⅰ)求a、b的值;
(Ⅱ)设M、N是右准线l上两动点,满足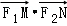
正确答案
(I)因为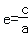
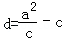
所以由题设得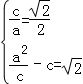
解得,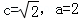
由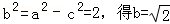
(Ⅱ)证明:由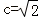
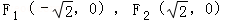
则l的方程为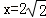
故可设
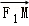
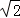
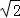
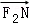

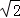
由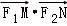
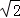
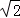
得y1y2=﹣6,所以y1y2≠0,
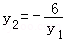
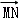


当且仅当
即M,N两点关于x轴对称.
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数f(x)=x3+ax2+bx+c的图象经过原点,且在x=1处取得极大值.
(Ⅰ)求实数a的取值范围;
(Ⅱ)若方程f(x)=﹣
(Ⅲ)对于(2)中的函数f(x),若对于任意实数α和β恒有不等式|f(2sinα)﹣f(2sinβ)|≤m成立,求m的最小值.
正确答案
(Ⅰ)f(0)=0⇒c=0,f'(x)=3x2+2ax+b,f'(1)=0⇒b=﹣2a﹣3,
∴f'(x)=3x2+2ax﹣(2a+3)=(x﹣1)(3x+2a+3),
由f'(x)=0⇒x=1或
因为当x=1时取得极大值,所以
所以a的取值范围是:(﹣∞,﹣3);
(Ⅱ)由下表:
画出f(x)的简图:
依题意得:
解得:a=﹣9,
所以函数f(x)的解析式是:f(x)=x3﹣9x2+15x;
(Ⅲ)对任意的实数α,β都有﹣2≤2sinα≤2,﹣2≤2sinβ≤2,
依题意有:函数f(x)在区间上的最大值与最小值的差不大于m,
在区间上有:f(﹣2)=﹣8﹣36﹣30=﹣74f(1)=7,
f(2)=8﹣36+30=2f(x)的最大值是f(1)=7,
f(x)的最小值是f(﹣2)=﹣8﹣36﹣30=﹣74,
所以m≥81即m的最小值是81.
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数f(x)=2sinxcosx+cos2x.
(Ⅰ)求f (
(Ⅱ)设α∈(0,


正确答案
(Ⅰ)∵f(x)=sin2x+cos2x,∴f(


(Ⅱ)∵f(

∴1+sin2α=

∴cos2α=
∵α∈(0,
∴2α∈(π,
∴cos2α<0.
故cos2α=
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,在四棱柱ABCD﹣A1B1C1D1中,AB=BC=CA=
(Ⅰ)求证:BD⊥AA1;
(Ⅱ)求证:A1E∥平面DCC1D1
(Ⅲ) 若AA1⊥AC,求A1E与面ACC1A1所成角大小.
正确答案
(Ⅰ)证明:在四棱锥ABCD﹣A1B1C1D1中,
∵AB=BC=CA,且AD=DC,
取AC中点O,则BO⊥AC,DO⊥AC,∴B,O,D三点在一条直线上.
又∵面AA1C1C⊥面ABCD,面AA1C1C∩面ABCD=AC,BD⊂面ABCD,BD⊥AC,
∴BD⊥面AA1C1C,AA1⊂面AA1C1C,∴BD⊥AA1;
(Ⅱ)证明:连AE,在Rt△DCO中∠DCO=30°
在正△BCA中,∠BCO=60°,∴DC⊥BC,
又在正△BCA中,AE⊥BC,
∴AE∥DC,
又AE⊄面DCC1D1,DC⊂面DCC1D1,∴AE∥面DCC1D1,
在四棱锥中,AA1∥DD1,AA1⊄面DCC1D1,DD1⊂面DCC1D1,
∴AA1∥面DCC1D1,
又AA1∩AE=A,
∴面A1AE∥面DCC1D1,
又A1E⊂面AA1E,故A1E∥面DCC1D1.
(Ⅲ)解:过E作AC的垂线,设垂足为N,∵面ABCD⊥面AA1C1C,∴EN⊥面AA1C1C,
连A1N,则A1N为A1E在面AA1C1C内的射影,
∴∠EA1N为直线A1E与面AC1所成角,
由已知得:

解析
解析已在路上飞奔,马上就到!