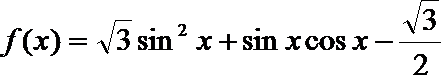- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合M={x|
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知圆




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.一空间几何体按比例绘制的三视图如图所示(单位:m),则该几何体的体积(单位:m3)为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.复数z=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知直线ax+4y-2=0与2x-5y+b=0垂直,垂足为(1,c)则a-b+c的值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若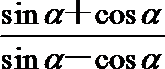

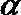
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知等差数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设f(x)是定义在R上以2为周期的偶函数,已知x∈(0,1)时,f(x)=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.点P在曲线y=


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设O为坐标原点,点M(2,1),点N(x,y),满足


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数y=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在平面直角坐标系中,定义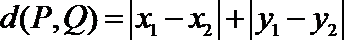
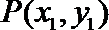
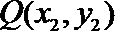
①到原点的“折线距离”等于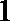
②到原点的“折线距离”等于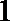
③到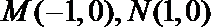
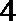

④到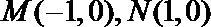
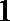
其中正确的命题是____________.(写出所有正确命题的序号)
正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数f(x)=2sin(ωx+

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在数列

(1)求数列
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
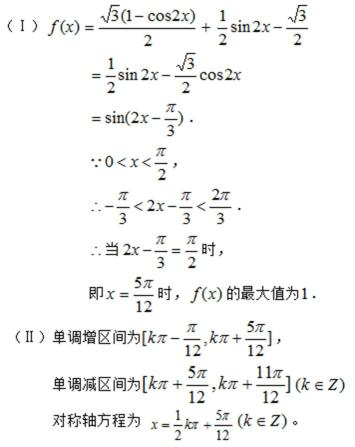
18. 已知函数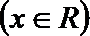
(Ⅰ)若
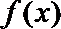
(Ⅱ)求函数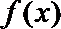
(Ⅲ)在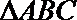
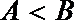
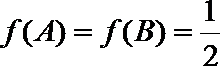
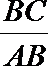
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
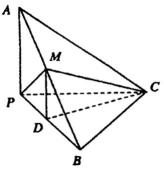
19.如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
(Ⅰ)求证:DM∥平面APC;
(Ⅱ)求证:平面ABC⊥平面APC;
(Ⅲ)若BC=4,AB=20,求三棱锥D-BCM的体积.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数f(x)=a

(1)求f(x)的解析式;
(2)若对任意的x∈[ 


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 设椭圆



(Ⅰ)试求椭圆的方程;
(Ⅱ)过F1、F2分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),若四边形DMEN的面积为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题记分.
22.选修4-1:几何证明选讲
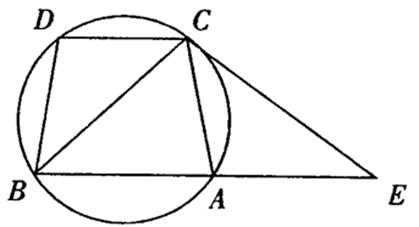
如图,ABDC是圆的内接四边形,AB∥CD,过C点的圆的切线与BA的延长线交于E点,证明:
(Ⅰ)∠DBC=∠AEC:
(Ⅱ)BC2=BE·CD.
23.选修4-4:坐&标系与参数方程
已知在平面直角坐标系xOy内,点P(x, y)在曲线C: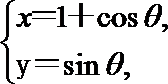
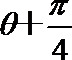
(Ⅰ)写出曲线C的标准方程和直线的直角坐标方程;
(Ⅱ)若直线与曲线C相交于A、B两点,点M在曲线C上移动,试求△ABM面积的最大值.
24.选修4—5:不等式选讲
已知关于x的不等式:|2x-m|≤1的整数解有且仅有一个值为2.
(Ⅰ)求整数m的值:
(Ⅱ)在(Ⅰ)的条件下,解不等式:|x-1|+|x-3|≥m.
正确答案
22.
23.
24.
解析
解析已在路上飞奔,马上就到!