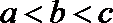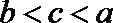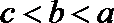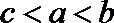- 真题试卷
- 模拟试卷
- 预测试卷
2.定义映射

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.下列函数中既是奇函数又在区间 
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设全集



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知命题

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若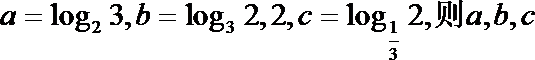
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知命题







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若存在负实数使得方程 

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数



正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
16.用




①

②
③
④
其中正确命题的序号是:________________.
正确答案
③
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数





正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
14.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数





(1)求
(2)设函数



正确答案
(1) 


又 
(2)由函数

可得函数



当
故函数


由

即




解析
解析已在路上飞奔,马上就到!
知识点
19.已知定义域为R的函数
(1)求a的值;
(2)判断
(3)若对任意的


正确答案
(1)函数
因为

即
故
(另解:由
所以

再由
通过验证

(2)解法一:由(1)知
由上式易知
(3)又因
从而不等式

即对一切
从而
解析
解析已在路上飞奔,马上就到!
知识点
17.已知


正确答案
对P:
对Q:由已知得f(x)=3x2+2mx+m+
Δ=4m2-12(m+
得m<-1或m>4.
所以,要使“P或Q”为真命题,只需求其反面,P假且Q假,
即

解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)若

(2)若

正确答案
(1)

即
则必有
(2)依题意,
即
令
得
当


解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数









(1)求函数
(2)记


正确答案
(1)由已知可得函数

方法一:由
得
得
方法二:设
由
(2)
列表可得
即
解析
解析已在路上飞奔,马上就到!