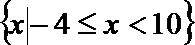- 真题试卷
- 模拟试卷
- 预测试卷
1.已知复数

正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
2.设集合

正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
3.设A,B是


正确答案

解析
解析已在路上飞奔,马上就到!
知识点
4.若实数


正确答案
9
解析
解析已在路上飞奔,马上就到!
知识点
5. 一几何体的主视图、左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知







正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
8. 设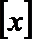
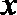
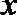
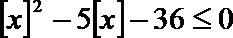
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.矩阵变换式



正确答案
16
解析
解析已在路上飞奔,马上就到!
知识点
10. 一只蚂蚁在三边边长分别为3,4,5的三角形的边上爬行,某时刻该蚂蚁距离三角形的三个顶点的距离均超过
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.执行下边的程序框图,若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰快,容器内盛有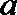
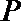
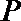
(1)任意摆放该容器,当水面静止时,水面都恰好经过点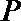
(2)正四棱锥的高等于正四棱柱的高的一半;
(3)若往容器内再注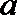
(4)将容器侧面水平放置时,水面也恰好过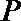
其中真命题的代号为 ( )。
正确答案
(3)(4)
解析
解析已在路上飞奔,马上就到!
知识点
12.等边三角形





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.将
这个正方形就叫做n阶幻方,如图就是一个3 阶幻方,定义f(n)为n阶幻方对角线上数的和,例如f(3)=15,则f(4)=______________
正确答案
34
解析
解析已在路上飞奔,马上就到!
知识点
15.在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.某商场在国庆黄金周的促销活动中,对10月2号9时至14时的销售额进行统计,其频率分布直方图如图1所示.已知9时至10时的销售额为2.5万元,则11时至12时的销售额为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.长方体


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.点

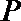
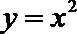
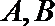
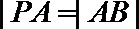
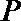
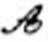
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数

(1)求
(2)若不等式


正确答案
(1)
又



(2)






解析
解析已在路上飞奔,马上就到!
知识点
20.已知:正方体


(1)求证:
(2)求证:

(3)求三棱锥
正确答案
(1)证明:连结


∵




又


∵


∴
(2)取

∴四边形

∴


(3)

解析
解析已在路上飞奔,马上就到!
知识点
21.设函数

(1)若


(2)设





正确答案
(1)
由
解得
(2)

当



因此当
解析
解析已在路上飞奔,马上就到!
知识点
22.已知双曲线




(1)求动点P的轨迹E的方程;
(2)设过

正确答案
(1)双曲线的方程可化为

∴P点的轨迹E是以
由
(2)略
解析
解析已在路上飞奔,马上就到!
知识点
23.已知以a为首项的数列
(1)若0<

(2)若a,k∈N﹡,求使
(3)若


正确答案
(1)当



故


(2)①当


同理可得,当

当

②当

③当
综上得:当

当

(3)由m


当





解析
解析已在路上飞奔,马上就到!