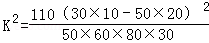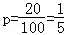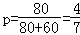- 真题试卷
- 模拟试卷
- 预测试卷
4.下列函数中是奇函数,且在区间(0,+∞)上单调递增的是( )
正确答案
解析
略
知识点
7.如图所示,使用模拟方法估计圆周率值的程序框图,P表示估计的结果,则图中空白框内应填入P=( )
正确答案
解析
略
知识点
8.已知{an}为等差数列,若a1+a5+a9=π,则cos(a2+a8)的值为( )
正确答案
解析
略
知识点
1.设集合M={x∈R|lgx=0},N={x∈R|﹣2<x<0},则( )
正确答案
解析
略
知识点
2.设复数z=﹣1﹣i(i为虚数单位),z的共轭复数为

正确答案
解析
略
知识点
9.已知函数f(x)=
正确答案
解析
略
知识点
3.命题“∀x∈R,x2+x≥2”的否定是( )
正确答案
解析
略
知识点
6.一个半径为2的球体经过切割后,剩余部分几何体的三视图如图所示,则该几何体的体积为( )
正确答案
解析
略
知识点
10.在△ABC中,若角A,B,C所对的三边a,b,c成等差数列,给出下列结论:
①b2≥ac;
②
③
④
其中正确的结论是( )
正确答案
解析
略
知识点
5.甲,乙,丙,丁四位同学各自对A,B两变量的线性相关试验,并用回归分析方法分别求得相关系数r如表:
则这四位同学的试验结果能体现出A,B两变量有更强的线性相关性的是( )
正确答案
解析
略
知识点
11.设x、y满足约束条件: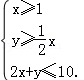
正确答案
-6
解析
略
知识点
12.记集合A={(x,y)|x2+y2≤4}和集合B={(x,y)|x+y﹣2≤0,x≥0,y≥0}表示的平面区域分别为Ω1和Ω2,若在区域Ω1内任取一点M(x,y),则点M落在区域Ω2的概率为 .
正确答案
解析
略
知识点
13.在极坐标系中,点(1,0)到直线ρ(cosθ+sinθ)=2的距离为 .
正确答案
解析
略
知识点
15.已知偶函数f(x)满足f(x+1)=-
正确答案
解析
略
知识点
14.已知抛物线y2=2px的焦点F与双曲线


正确答案
32
解析
略
知识点
21.在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别是(﹣

(1)求△ABC的顶点C的轨迹E的方程;
(2)不过点A的直线l与轨迹E交于不同的两点P,Q.若以PQ为直径的圆过点A时,试判断直线l是否过定点?若过,请求出定点坐标,不过,说明理由.
正确答案
见解析。
解析
(1)设点C坐标为(x,y)
因为G为△ABC的重心故G点坐标为
由|MC|=|MB|得∴
即
∴△ABC的顶点C的轨迹E的方程是
(2)设直线
联立:
∴△=4k2b2﹣4(k2+3)(b2﹣6)=12(2k2﹣b2+6)>0,
且
若以PQ为直径的圆过点A时,则有
∴

故
代入整理得:

①当


且代入△>0成立; …(13分)
②当

综上知:直线过定点
知识点
16.在锐角△ABC中,角A,B,C的对边分别为a,b,c且sin2A﹣cosA=0.
(1)求角A的大小;
(2)若b=

正确答案
(1)
(2)a=1
解析
(1)由sin2A﹣cosA=0,得2sinAcosA﹣cosA=0,
即cosA(2sinA﹣1)=0得cosA=0或sinA=
∵△ABC为锐角三角形,
∴sinA=
则A=
(2)把sinB=

∵b=
由余弦定理得:a2=b2+c2﹣2bccosA=3+1﹣2×

解得:a=1.
知识点
18.在△ABC中(如图1),已知AC=BC=2,∠ACB=120°,D,E,F分别为AB,AC,BC的中点,EF交CD于G,把△ADC沿CD折成如图2所示的三棱锥C﹣A1BD.
(1)求证:E1F∥平面A1BD;
(2)若二面角A1﹣CD﹣B为直二面角,求直线A1F与平面BCD所成的角.
正确答案
见解析。
解析
(1)证明:E1,F分别为AC,BC的中点,
则E1F为A1BC的中位线,
故E1F∥A1B
因为A1B⊂面A1BD,E1F⊄平面A1BD,
所以E1F∥平面A1BD.
(2)连结DF,∵二面角A1﹣CD﹣B为直二面角,
∴A1D⊥BD,
又∵AC=BC且D为AB的中点,∴A1D⊥CD,
得A1D⊥平面BDC,
故∠A1FD为直线A1F与平面BCD所成的角
在△ABC中,AC=BC=2,∠ACB=120°,
得CD=1,CF=1,∠DCF=60°
∴△CDF为等边三角形,
故DF=1,
则
故直线A1F与平面BCD所成的角为60°.
知识点
19.已知数列{an}是正数等差数列,其中a1=1,且a2、a4、a6+2成等比数列;数列{bn}的前n项和为Sn,满足2Sn+bn=1.
(1)求数列{an}、{bn}的通项公式;
(2)如果cn=anbn,设数列{cn}的前n项和为Tn,是否存在正整数n,使得Tn>Sn成立,若存在,求出n的最小值,若不存在,说明理由.
正确答案
见解析。
解析
(1)设数列{an}的公差为d,
∵a1=1,且a2、a4、a6+2成等比数列,
∴依条件有
即

所以an=a1+(n﹣1)d=1+(n﹣1)=n.
由2Sn+bn=1,得
当n=1时,2S1+b1=1,解得
当n≥2时,
所以
所以数列{bn}是首项为

故
(2)由(1)知,
所以

得
又
所以
当n=1时,T1=S1,
当n≥2时,
故所求的正整数n存在,其最小值是2.
知识点
20.已知函数f(x)=
(1)当a=1时,求f(x)的最小值;
(2)若f(x)在(0,e]上的最小值为2,求实数a的值;
(3)当a=﹣1时,试判断函数g(x)=f(x)+
正确答案
(1)1
(2)a=e
(3)见解析。
解析
(1)当a=1时,
当x∈(0,1)时,f′(x)<0,f(x)单调递减,
当x∈(1,+∞)时,f′(x)>0,f(x)单调递增,
所以,当x=1时,f(x)有最小值:f(x)min=f(1)=1.
(2)因为
①当a≤0时,f′(x)>0,f(x)在(0,e]上为增函数,此时f(x)在(0,e]上无最小值.
②当a∈(0,e]时,若x∈(0,a),则f′(x)<0,f(x)单调递减,
若x∈(a,e],则f′(x)>0,f(x)单调递增,
所以f(x)min=f(a)=1+lna=2,∴a=e,符合题意;
③当a>e时,x∈(0,e],
∴f′(x)<0,f(x)单调递减,
所以
∴a=e,不符合题意;
综上所述,a=e时符合题意.
(3)证明:当a=﹣1时,函数

令φ(x)=2+x﹣lnx,(x>0),则
所以x∈(0,1)时,φ′(x)<0,φ(x)单调递减,
当x∈(1,+∞)时,φ′(x)>0,φ(x)单调递增,
所以,φ(x)min=φ(1)=3>0,在定义域内g′(x)>0,g(x)在(0,+∞)单调递增,
又g(1)=﹣1<0,而
因此,函数g(x)在(1,e)上必有零点,又g(x)在(0,+∞)单调递增,
所以函数
知识点
17.为了解甲、乙两种品牌手机的电池充满电后的待机时间(假设都在24~96小时范围内),从这两种手机的电池中分别随机抽取100个进行测试,结果统计如下表.
(1)估计甲品牌手机的电池充满电后的待机时间小于48小时的概率;
(2)这两种品牌的手机的电池充满电后,某个电池已使用了48小时,试估计该电池是甲品牌手机的电池的概率;
(3)由于两种品牌的手机的某些差异,普遍认为甲品牌手机比乙品牌手机更显“低调”,销售商随机调查了110名购买者,并将有关数据整理为不完整的2×2列联表,写出表中A、B、C、D、E的值,并判断是否有99%的把握认为喜欢“低调型”手机与消费者的年龄有关?
附:K2=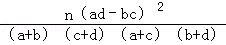
正确答案
见解析。
解析
(1)甲品牌手机的电池充满电后的待机时间小于48小时的频数是20,共有100个,
所以,甲品牌手机的电池充满电后的待机时间小于48小时的概率
(2)两种品牌的手机的电池充满电后,可以使用48小时分别是80个和60个,所以,某个电池已使用了48小时,该电池是甲品牌手机的电池的概率
(3)A=20,B=50,C=80,D=30,E=110,H0:假设是否喜欢“低调型”手机与消费者的年龄无关,根据列联表可得: