- 真题试卷
- 模拟试卷
- 预测试卷
3.下列命题,真命题的是
正确答案
解析

考查方向
解题思路
逐一进行判断,找到正确答案,可以通过举反例推翻。
易错点
对概率不是很理解。
知识点
5.右图是计算
判断框内可以填的是
正确答案
解析
因为是先计算再累加,所以
考查方向
解题思路
按照要求,最终判断跳出循环的时候刚好要符合题意即可。
易错点
条件判断失误。
知识点
7. 直角三角形ABC中,A=90°,B=60°,B,C为双曲线E的两个焦点,点A在双曲线E
正确答案
解析
由题意知两个焦点之间的距离为2c,因为A=90°,B=60°,所以AB=c,AC=


考查方向
解题思路
利用已知条件再结合双曲线的定义得到a,b,c的一个方程,再求出离心率。
易错点
不能想出利用双曲线的定义来解答。
知识点
10.已知函数





正确答案
解析









考查方向
解题思路
求出两个函数的零点,再去找到要求的最小值。
易错点
不知道怎么转化为所学知识来解答。
知识点
1.设集合
正确答案
解析


考查方向
解题思路
求出A集合,然后计算出两个集合的交集。
易错点
A集合取反。
知识点
2.已知i是虚数单位,复数
正确答案
解析

考查方向
解题思路
直接计算。
易错点
粗心出现错误。
知识点
4.已知

正确答案
解析


考查方向
解题思路
先将要求的模平方,利用2个向量是单位向量并且垂直即可算出。
易错点
向量的求模方法忘记。
知识点
6.已知函数

正确答案
解析


考查方向
解题思路
先分别将两个函数化简,然后找到正确答案。
易错点
不记得辅助角公式。
知识点
8.下列关于空间的直线和平面的叙述,正确的是
正确答案
解析
A答案还可以为相交和异面,B答案中的两个平面还可以相交,D答案中的两个平面的位置关系还可以是平行的,所以正确答案是C.
考查方向
解题思路
可以逐一进行判断找到正确的答案。
易错点
判断出错。
知识点
9. 如图是抛物线形拱桥,当水面在时,拱

正确答案
解析
建立适当的坐标系,以顶点为坐标原点,抛物线开口向下,可设为




考查方向
解题思路
建立直角坐标系,然后计算出抛物线的方程,然后即可解出水面的宽。
易错点
不知道建立坐标系来求解。
知识点
11.计算
正确答案

解析
考查方向
解题思路
本题考查先利用诱导公式化简,然后利用2倍角公式即可解出。
易错点
公式记错。
知识点




正确答案
12. 8;
解析
如图所示,当经过点(2,4)时取到目标函数
考查方向
解题思路
本题考查简单线性规划问题,先做出可行域,再通过数形结合法找到最大值。
易错点
不知道经过可行域中的什么位置取到最大值。
知识点
13.某几何体的三视图如右图所示,其中正视图和俯视图均为全等的正方形(边长为2),侧视图为等腰直角三角形(直角边的长为2),则该几何体的表面积是 .
正确答案
解析
如图所示,几何体是一个三棱柱,所以其表面积为
考查方向
解题思路
本题考查根据三视图找到直观图,再计算出其表面积。
易错点
直观图弄错。
知识点
14.过点(-1, 0)的直线l与圆C:
正确答案
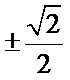
解析
设过点(-1, 0)的直线方程为y=k(x+1),因为△ABC为等边三角形,


考查方向
解题思路
本题利用三角形是等边三角形最后求出斜率。
易错点
不会转化为所学知识来解答。
知识点
15.已知函数
① 函数
② 函数
③ 函数




其中所有真命题的序号是 .
正确答案
①③.
解析
根据函数的性质知道,




考查方向
解题思路
本题考查采用正确的方法去逐一判断找到正确答案。
易错点
不会解答。
知识点
16. 在△ABC中,角A,B,C的对边分别为a,b,c,向量

(Ⅰ)求角
(Ⅱ)若a=6,求△ABC面积的最大值.
正确答案
(1)

解析
试题分析:本题属于向量结合三角函数以及解三角形的知识
(1)根据向量共线的坐标表示得到一个等式,再利用正弦定理实现边角互化从而可以解出角A;
(2)先由余弦定理再结合基本不等式即可。
(Ⅰ)因为向量

所以

即
由于B是三角形的内角,


(Ⅱ)因为
所以
且仅当b=c时取得等号,所以

所以当b=c时,△ABC面积的最大值为
考查方向
解题思路
本题考查向量结合三角函数以及解三角形的知识,解题步骤如下:
(1)根据向量共线的坐标表示得到一个等式,再利用正弦定理实现边角互化从而可以解出角A;
(2)先由余弦定理再结合基本不等式即可。
易错点
不能联想到基本不等式。
知识点
17. 人的体重是人的身体素质的重要指标之一.某校抽取了高二的部分学生,测出他们的体重(公斤),体重在40公斤至65公斤之间,按体重进行如下
(Ⅰ)求该校抽取的学生总数以及第2组的频率;
(Ⅱ)学校为进一步了解学生的身体素质,在第1
正确答案
(1)0.25;(2)
解析
试题分析:本题属于平率分布直方图及古典概型的应用,
(1)直接按照步骤来求;
(2)根据古典概型的公式来计算。
(Ⅰ)设该校抽查的学生总人数为n,第 2组、第3组的频率分别为

则



所以该校抽查的学生总人数为240人,从左到右第2组的频率为0.25
(Ⅱ)前3组的频率之比是1 : 2 : 3,则按照分层抽样,这6人的构成是第1组1人(不妨设为A),第2组2人(不妨设为



所以这2人来自同一组的概率
考查方向
解题思路
本题考查平率分布直方图及古典概型的应用,解题步骤如下:(1)直接按照步骤来求;根据古典概型的公式来计算。
易错点
误将图像的纵坐标当做频率。
知识点
20.已知椭圆E:

(Ⅰ)求椭圆
(Ⅱ)直线l与椭圆E相交于A,B两个不同的点,线段AB的中点为C,O为坐标原点,若△OAB面积为

正确答案
(1)
解析
试题分析:本题属于直线与椭圆的位置关系,题目的难度是逐渐由易到难,
(1)直接根据题意构造方程组来求解;
(2)分斜率存在和不存在2种情况分类讨论,再利用设而不求的方法来计算出最小值。
(Ⅰ)由题

所以椭圆E的方程为
(Ⅱ)(1)当l的斜率不存在时,A,B两点关于x轴对称,则

由




可知

(2)当l的斜率存在时,设直线l:
联立方程组

由

则


原点O到直线l的距离
△OAB的面积


所以


可知


则C

由于



综上所述,

考查方向
解题思路
本题考查直线与椭圆的位置关系,解题步骤如下:
(1)直接根据题意构造方程组来求解;
(2)分斜率存在和不存在2种情况分类讨论,再利用设而不求的方法来计算出最小值。
易错点
第2问计算量大容易出错。
知识点
18. 已知数列


(Ⅰ)求

(Ⅱ)设



正确答案
(1)


解析
试题分析:本题属于等差数列及数列的求和,
(1)直接利用公式来解答;
(2)先利用裂项相消法求出
(Ⅰ)设数列


由

所以

(Ⅱ)可得

由于

即

考查方向
解题思路
本题考查等差数列及数列的求和,解题步骤如下:(1)直接利用公式来解答;(2)先利用裂项相消法求出
易错点
第二问求和不晓得使用裂项相消法去做。
知识点
19. 如图,在三棱锥P-AMC中,AC=AM=PM=2,PM⊥面AMC,AM⊥AC,B,D分别为CM,AC的中点.
(Ⅰ)在PC上确定一点E,使得直线PM∥平面ABE,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,连接AE,与PD相交于点N,求三棱锥B-ADN的体积.
正确答案
(1)E为PC的中点;(2)
解析
试题分析:本题属于立体几何证明与求体积的问题,(1)利用线面垂直的判定定理来证明;(2)将体积最终转化为
(Ⅰ)E为PC的中点.理由如下:
连接BE,由于B,E分别为CM,PC的中点,
所以BE∥PM,
又BE

所以PM∥面ABE.
(Ⅱ)由于AE,PD分别是△PAC的边PC,AC上的中线,所以AE和PD的交点N为△PAC的重心,故N为PD靠近D的三等分点,
则
而因为D为AC的中点,所以
又由于E为PC的中点,
所以
所以三棱锥B-AND的体积为
考查方向
解题思路
本题考查立体几何证明与求体积的问题,解题步骤如下:
(1)利用线面垂直的判定定理来证明;
(2)将体积最终转化为
易错点
求体积的时候不会转化。
知识点
21.已知函数
(Ⅰ)当

(Ⅱ)若函数

(Ⅲ)当




注:题目中e=2.71828…是自然对数的底数.
正确答案
(1)



解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,
(1)利用导数直接做;
(2)转化为求函数的最值。
(3)利用导数这个工具来解答。
(Ⅰ)当





所以切线l的方程为
(Ⅱ)由题知

令



则当

由


(Ⅲ)

由题



当1<x<e时,

因为


所以
同理
①+②得
因为
且由





所以
所以

考查方向
解题思路
本题考查导数的性质,解题步骤如下:
(1)利用导数直接做;
(2)转化为求函数的最值。
(3)利用导数这个工具来解答。
易错点
求参数的取值范围不会转化为求函数的最值。
























































