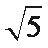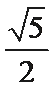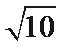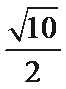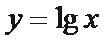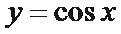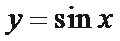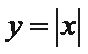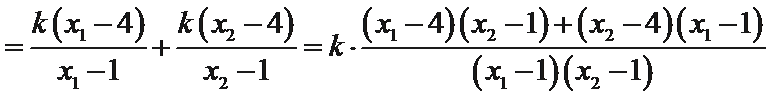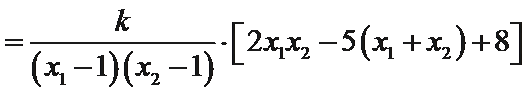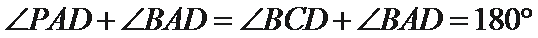文科数学桂林市2016年高三第一次联合考试

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

2．复数（）

正确答案

解析

，所以选择C选项.

考查方向

本题主要考查了复数的运算,复数的运算在近几年各省的高考题中几乎每年都会出现，需要高度重视。

解题思路

根据复数的乘法、除法运算直接计算即可得到结果。

易错点

复数的运算题目一般比较容易，往往会在计算时因失误而失分，本题容易因为这一知识点不清楚而出现错误。

知识点

复数的代数表示法及其几何意义

题型：单选题

分值: 5分

3．等差数列{an}中，a4+a8=10，a10=6，则公差d等于（）

正确答案

解析

由以及等差数列的通项公式可知：，解得.因此选择A选项。

考查方向

本题主要考查了等差数列的通项公式，同时考查了解方程组的能力，题目难度较低。

解题思路

根据题目条件联立方程组即可直接求解。

易错点

没有记清楚等差数列的通项公式是导致本题出错的主要原因。

知识点

等差数列的判断与证明

题型：单选题

分值: 5分

4．已知函数则（）

正确答案

解析

因为2>1,所以，此时由于=-1<0，因此，所以选A选项。

考查方向

本题主要考查了对分段函数的理解以及对复合函数的认识、分段函数在近几年的各省高考题出现的频率较高。

解题思路

根据复合函数的运算规则，从内层函数出发，逐层往外计算，因此先算，然后再算.

易错点

本题易在不理解的含义而导致错误。

知识点

不等式的性质

题型：单选题

分值: 5分

7．如图是一个空间几何体的三视图，其中正视图、侧视图都是由边长为4和6的矩形以及直径等于4的圆组成，俯视图是直径等于4的圆，该几何体的体积是（）

正确答案

解析

该三视图所对应的空间几何体是一个圆柱上面放一个球，根据圆柱和球的体积计算公式可知，所以选D选项。

考查方向

本题主要考查了三视图以及空间几何体的体积计算公式，三视图是新课改中新增的知识，在近几年的各省高考题中几乎每年都会出现，常与空间几何体的表面积和体积交汇命题。

解题思路

1、首先根据三视图还原出原来的几何体；

2、根据空间几何体的体积计算公式选择合适的公式计算。

易错点

不能根据三视图准确地还原出原来的空间几何体而导致本题不会做。

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

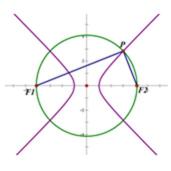
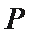
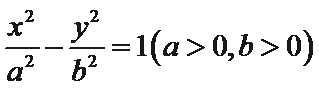
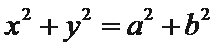
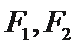
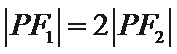
11．设点是双曲线与圆在第一象限的交点，分别是双曲线的左、右焦点，且，则双曲线的离心率为（）

正确答案

解析

根据题意易知圆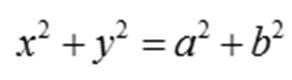与坐标轴的焦点恰好是双曲线的两个焦点（如图所示：），

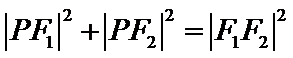
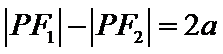
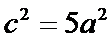
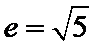
由此可知三角形为直角三角形，因此,再由双曲线的定义可知,由上述两式可得，因此离心率，所以本题选择A选项。

考查方向

本题主要考查了双曲线的定义、标准方程以及相关的几何性质、圆的性质等知识点，同时考查了综合法、转化法等思想方法以及学生的计算能力。

解题思路

画出草图，结合图形通过题目条件确定a与c的代数关系，即可求出双曲线的离心率。

易错点

本题容易因为对双曲线的定义不会应用而导致题目不会做。

知识点

双曲线的定义及标准方程

题型：单选题

分值: 5分

1．已知全集，集合，则（）

正确答案

解析

,因此，所以选择A选项.

考查方向

本题主要考查了集合的交、补运算,集合的基本运算在近几年的各省高考题出现的频率较高，常与不等的解法交汇命题，考生应引起重视。

解题思路

先根据补集的定义求出集合，然后根据集合的交运算求出相应的结果。

易错点

本题容易因为忽略端点处的“1”不能取这一细节而导致误选C。

知识点

交集及其运算

题型：单选题

分值: 5分

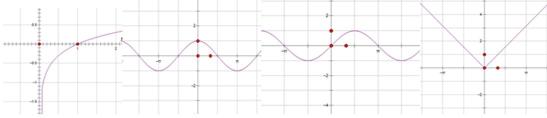
5．下列函数中，图象关于坐标原点对称的是（）

正确答案

解析

思路1:四个函数的图像如下，易知选择C。

思路2：的定义域为，定义域不关于原点对称，不是奇函数；

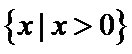
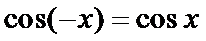
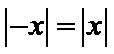
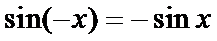
其余三个函数的定义域都关于原点对称，但是、，因此B、D选项中的函数均为偶函数，只有，因此选择C选项。

考查方向

本题主要考查了一些简单函数的图像的对称性（奇偶性）问题题目难度较小。

解题思路

1、直接利用记忆中这些函数的图像特征进行判断；

2、通过判断函数的单调性进行判断；

易错点

本题容易因为没有记清楚这些函数的图像特征而出现错误。

知识点

函数奇偶性的性质奇偶函数图象的对称性

题型：单选题

分值: 5分

6．已知，则（）

正确答案

解析

，所以选D选项。

考查方向

本题主要考查了同角三角函数的基本关系式，诱导公式以及三角恒等变换问题，考查了转化化归思想方法。

解题思路

首先由利用诱导公式将进行化简，然后通过三角恒等变换可以求得最终结果。

易错点

1、本题易在使用诱导公式时判断错误符号而导致出错。

2、本题容易因为公式记忆不清楚而出现错误。

知识点

三角函数恒等式的证明求函数y＝Asin(ωx＋φ)的解析式

题型：单选题

分值: 5分

8．已知如图所示的程序框图，那么输出的（）

A45

B35

C21

D15

正确答案

解析

过程见下表：

考查方向

本题主要考查了算法与程序框图，主要考查了直到型循环结构。

解题思路

根据程序框图探索该程序所要解决的问题，然后利用所学知识求解，由于本题退出条件较简单，因此可以逐步探索。

易错点

本题容易对循环退出的条件判断不准确而出现错误，往往会在计算时因失误而失分。

知识点

顺序结构

题型：单选题

分值: 5分

10．已知向量与的夹角为，且，，若，且，则实数的值为（）

B13

正确答案

解析

，解得，因此选择D选项。

考查方向

本题主要考查了向量的减法、数量积运算以及两个向量垂直的充要条件，同时考查了转化化归的数学思想方法，向量的数量积运算是高考中的常规性的题目，经常出现，需引起考生的注意。

解题思路

根据可知，然后再结合已知条件将转化,通过计算即可求解。

易错点

对向量的减法运算不熟练，不会转化而导致本题不会做。

知识点

相等向量与相反向量

题型：单选题

分值: 5分

12．已知函数，当（为自然常数），函数的最小值为3，则的值为（）

正确答案

解析

，

当时，，在上单调递减=3，得（舍）；

当时，在上单调递减，在上单调递增，，

得，满足条件；

当时，在上单调递减，，得（舍）；

综上可知，因此本题选择B选项。

考查方向

本题主要考查了导数在研究函数的单调性以及最值中的应用等知识，同时考查了分类讨论的数学思想方法。

解题思路

利用导数求解，首先求出导数，然后结合的取值范围进行分类讨论。

易错点

本题容易因为不能对的取值进行恰当的分类而导致做错。

知识点

导数的运算

题型：单选题

分值: 5分

9．函数的零点所在的区间是（）

正确答案

解析

画出函数y=lgx以及y=的图像，可以看到它们的零点在1的右侧，计算，此时y=lgx的图像在y=的图像的下方；，此时y=lgx的图像在y=的图像的下方，由此可以确定零点在区间（2,3）上。

考查方向

本题主要考查了函数的零点，同时考查了数形结合的数学思想方法。

解题思路

画出图像，确定大概位置，再通过估值的方式确定具体区间。

易错点

本题容易在估值时估算不准确而出现错误。

知识点

导数的乘法与除法法则

填空题本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 5分

15.若圆以抛物线的焦点为圆心，截此抛物线的准线所得弦长为6，则该圆的标准方程是_____

正确答案

解析

画出草图，如图所示，据图可知F（1,0）为圆心，BF=2，BC=3，由此可以求得CF=，所以圆的标准方程为。

考查方向

本题主要考查了抛物线的标准方程、相关的几何性质以及圆的标准方程等知识点，同时考查了数形结合、转化化归的数学思想方法。

解题思路

画出草图，

结合图形通过题目条件确定相应的几何关系关系，即可求出圆的半径即可。

易错点

本题容易因为对抛物线的标准方程记忆不清楚而导致题目做错。

知识点

两条直线垂直与倾斜角、斜率的关系

题型：填空题

分值: 5分

14.已知实数满足不等式组则的最小值为______．

正确答案

-4

解析

可行域如图所示，

据图可知，当经过区域右上角的点（2,3）时截距最大，取得最小值-4．

考查方向

本题主要考查了线性规划的相关知识。

解题思路

根据线性约束条件画出可行域。2、可的最小值可以理解为与直线平行的直线中，在y轴上截距最大时取得．

易错点

本题往往会因为不能准确地理解取得最小值时的位置而导致本题做错。

知识点

不等式的性质

题型：填空题

分值: 5分

16.已知四棱锥的顶点都在球上，底面是矩形，平面平面，为正三角形，，则球的表面为______．

正确答案

解析

令三角形PAD所在圆的圆心为P，则圆P的半径为，因为平面PAD与平面ABCD垂直，所以,所以球的半径为，所以求得表面积为。

考查方向

本题考查球的表面积的计算，同时考查了学生的空间想象能力。

解题思路

本题考查球的表面积的计算,关键是找出球心所在的位置并求出球的半径,本题利用了补体的思想,将棱锥补成棱柱,借助棱柱来寻找球心的位置.。

易错点

本题容易因为找不到球心的位置而导致题目不会做。

知识点

棱锥的结构特征

题型：填空题

分值: 5分

13．若函数为奇函数，则______．

正确答案

解析

因为为奇函数，所以，于是，所以，由此可以解得a=1.

考查方向

本题主要考查了函数奇偶性的应用，同时考查了学生的运算能力。

解题思路

利用奇函数的定义建立等式，然后求解。

易错点

本题容易因为奇函数的定理理解不清楚而导致错误。

知识点

变化的快慢与变化率

简答题（综合题）本大题共70分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

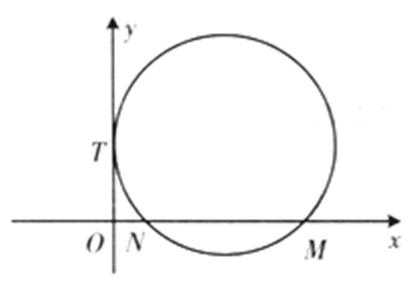
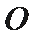
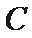
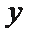
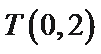
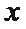
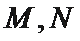
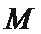
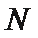
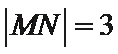
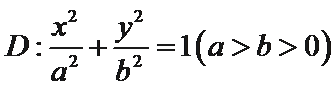
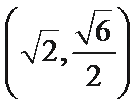
20．如图，已知为原点，圆与轴相切于点，与轴正半轴相交于两点（点在点的右侧），且；椭圆过点，且焦距等于．

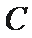
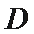
（1）求圆和椭圆的方程；

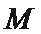
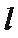
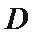
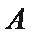
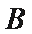
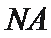
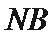
（2）若过点斜率不为零的直线与椭圆交于、两点，求证：直线与直线的倾斜角互补．

正确答案

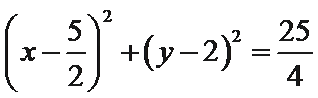
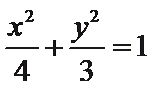
（1）圆的方程为：；椭圆的方程为：；

（2）略。

解析

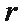
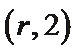
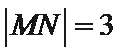
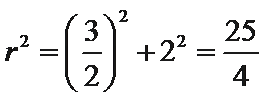
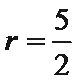
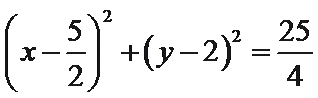
（1）设圆的半径为，由题意，圆心为，

∵，∴，．故圆的方程为．

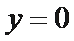
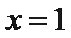
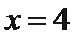
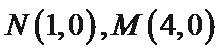
令，解得或，所以．

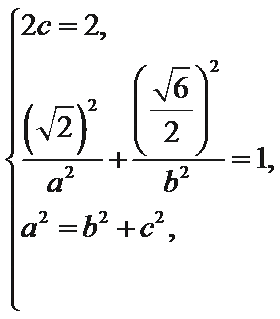
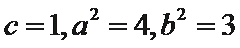
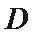
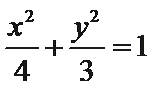
由得． ∴椭圆的方程为．

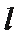
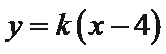
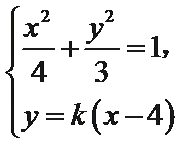
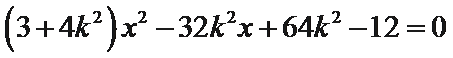
（2）设直线的方程为，由得

①

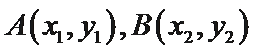
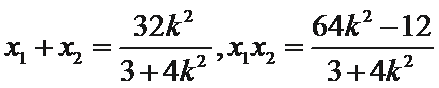
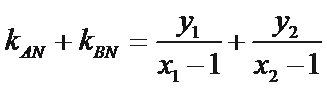
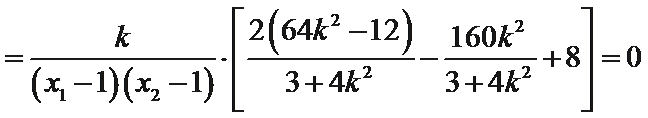
设，则．

∵

．

所以．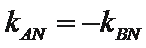

当或时，，此时方程①，，不合题意。

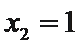
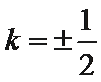
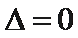
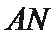
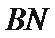
∴直线与直线的倾斜角互补．

考查方向

本题考查了圆与椭圆的标准方程与几何性质，直线与椭圆的位置关系等基础知识，同时考查了解析几何的基本思想方法和综合解题能力。

解题思路

1、第（1）问根据圆以及椭圆的标准方程，建立方程组，通过待定系数的方法即可求解；

2、第（2）问可以通过直线与椭圆的位置关系建立方程组，利用韦达定理求解；

易错点

本题容易因为对圆以及椭圆的相关性质掌握不清楚而导致不会做。

知识点

轨迹方程的问题

题型：简答题

分值: 12分

17．在中，内角、、对应的边长分别为、、，已知．

（1）求角；

（2）求的最大值．

正确答案

（1）；

（2）．

解析

试题分析：本题第（1）问属于解三角形的知识，是基础知识，难度中等；第（2）问是求三角式的值域的问题，解答过程如下：

（1）∵，由余弦定理得

∵，∴．

（2）

；

∵，∴，．

∴的最大值．

考查方向

本题考查了解三角形以及三角恒等变换的相关问题，主要考查了余弦定理、三角恒等变换等知识，同时考查了转化化归思想以及运算求解能力。

解题思路

1、第（1）问根据已知条件结合余弦定理可直接求出。

2、第（2）问用三角形的内角和定理以及辅助角公式进行转化，然后利用三角函数的值域的求法求的最大值。

易错点

本题容易因为忽略角的范围而导致错误的出现。

知识点

三角形中的几何计算

题型：简答题

分值: 12分

18．（某市教育部门规定，高中学生三年在校期间必须参加不少于80小时的社区服务．某校随机抽取20位学生参加社区服务的数据，按时间段，，，，（单位：小时）进行统计，其频率分布直方图如图所示．

（1）求抽取的20位学生中，参加社区服务时间不少于90小时的学生人数；

（2）从参加社区服务时间不少于90小时的学生中任意选取2人，求所选学生参加社区服务时间在同一时间段内的概率．

正确答案

（1）8;

（2）；

解析

解答过程如下：

（1）由题意可知，

参加社区服务在时间段的学生人数为（人）；

参加社区服务在时间段的学生人数为（人）．

所以参加社区服务时间不少于90小时的学生人数为人．

（2）设所选学生的服务时间在同一时间段内为事件，由（1）可知，

参加社区服务在时间段的学生有6人，记为；

参加社区服务在时间段的学生有2人，记为，

从这8人中任意选取2人有，，，，，共28种情况．

其中事件包括共16种情况．

∴所选学生的服务时间在同一时间段内的概率．

考查方向

本题考查了利用频率直方图求频数以及古典概型的知识，考查运用概率与统计的知识与方法分析和解决实际问题的能力，考查运算求解能力和应用意识，在新课程高考中经常性考查，需要引起考生的注意。

解题思路

1、根据频率分布直方图中求出利用以及上的人数，然后加起来。

2、先列举出所有的基本事件，然后分别统计在同一时间段内所包含的基本事件的个数，利用古典概型公式求解。

易错点

本题容易因对频率分布直方图的认识不到位而导致计算出错，在第二问中会因为列举不全而导致错误；

知识点

分布的意义和作用

题型：简答题

分值: 12分

19．在如图所示的多面体中，平面，平面，，，．

（1）在线段上取一点，作平面，（只需指出的位置，不需证明）；

（2）对（1）中，求三棱锥的体积．

正确答案

（1）略;

（2）；

解析

（1）取的中点，连接，平面（如图）．

（注：①作交于，作交于连，亦可满分．②按①作法，保留作图痕迹未作说明也得满分．）

（2）∵，∴，∴，

∵平面，∴．

∵，∴平面．

∵平面，平面，∴．

∵平面，平面，∴平面．

∴到平面的距离为．又，

∴．

考查方向

本题考查了空间点、线、面的位置关系以及空间几何体的体积问题，同时考查了空间想象能力和运算求解能力。

解题思路

1、第（1）问根据线面平行的条件，转化为面面平行的问题求解；

2、第（2）问关键是要求出B到平面FCD的距离，实际上是一个线面平行和线面垂直的综合性问题；

易错点

无法确定点B到平面FCD的距离而无法求解。

知识点

平面与平面平行的判定与性质

题型：简答题

分值: 10分

22．选修4-1：几何证明选讲

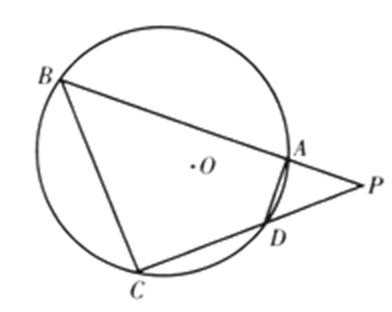
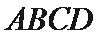
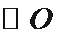
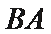
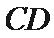
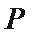
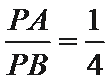
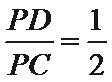
如图，四边形是的内接四边形，延长和相交于点，，．

（1）求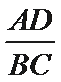的值；

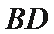
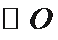
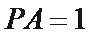
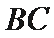
（2）若为的直径，且，求的长．

正确答案

（1）

（2）．

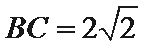
解析

试题分析：本题属于几何证明选讲中的基本问题，题目的难度一般，解题过程如下：

（1）∵

∴，，得与相似．

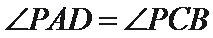
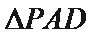
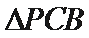
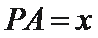
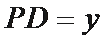
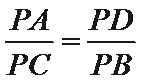
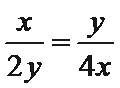
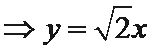
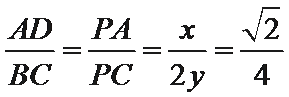
设，，则有，．

∴．

（2）由题意知，，，∴． ∴．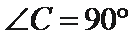

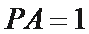
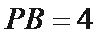
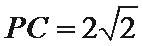
∴在中，，∴．

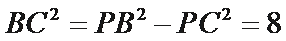
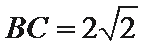
考查方向

本题考查了几何证明选讲的专题知识，考查了相似性的问题。

解题思路

本题考查几何证明选讲的相关知识，主要考查了相似性的问题，通过三角形相似即可求解。

易错点

对几何定理记忆不熟练，看不出图中的几何关系而导致做错。

知识点

二元二次方程表示圆的条件

题型：简答题

分值: 12分

21．已知函数．

（1）若函数在区间上为增函数，求的取值范围；

（2）当且时，不等式在上恒成立，求的最大值．

正确答案

（1）；

（2）。

解析

用导数研究函数的性质的问题，是导数题目中的常见问题；用导数作为工具来解决不等式问题，题目综合性较强，难度较大。解答过程如下：

（1），

由题意知在上恒成立，即在上恒成立，即在上恒成立，而，所以．

（2）．即对任意恒成立．

令，则．

令，则在上单调递增．

∵，∴存在使．

即当时，．即．

时，即．∴在上单调递减，在上单调递增．

令，即；

；

∴且，即．

请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分．

考查方向

本题考查了导数的运算、利用导数研究函数的性质、解决不等式问题等基础知识和方法，考查函数思想和化归思想，考查综合分析问题和解决问题的能力。

解题思路

1、第（1）问可以通过函数的单调性与导数的关系，通过解不等式求得的取值范围；

2、第（2）问可以通过转化化归的方法，将问题转化为函数的最大、最小值问题进行求解。

易错点

不会对问题进行等价转化而导致不会做。

知识点

变化的快慢与变化率

文科数学 热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

文科数学热门试卷