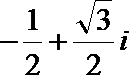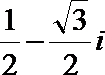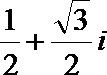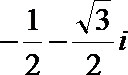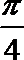- 真题试卷
- 模拟试卷
- 预测试卷
2. 已知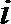
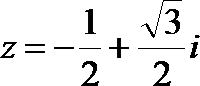
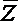
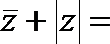
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 若函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 一个算法的程序框图如图所示,该程序输出的结果为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 实数x,y满足

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 一个组合体的主视图和左视图相同,如图,其体积为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 如果对定义在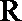
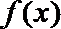


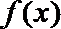

①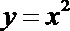
②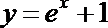
③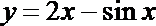
④
以上函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 已知数列{



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知
从散点图分析,



正确答案
-0.61
解析
解析已在路上飞奔,马上就到!
知识点
13. △ABC中,角A、B、C的对边分别为a,b,c,若S表示△ABC的面积,若acosB+bcosA=csinC,,且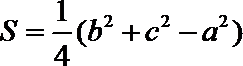
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知椭圆的左焦点为




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设M是△ABC的重心,若A=


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.数列







(1)求数列

(2)





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数

(Ⅰ)设曲线


(Ⅱ)当


(Ⅲ)令




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆



(Ⅰ)求椭圆
(Ⅱ)若直线









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
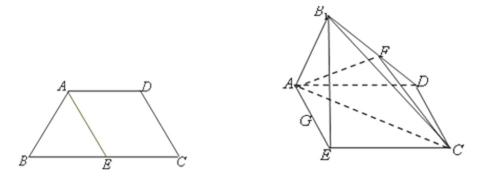
18.已知四边形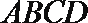
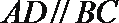
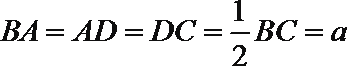
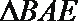
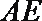
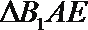
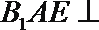
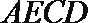
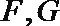
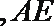
(Ⅰ)求三棱锥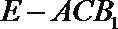
(Ⅱ)证明:平面
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,已知



(1)用

(2)设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.某区体育局组织篮球技能大赛,每名选手都要进行运球、传球、投篮三项比赛,每名选手在各项比赛中获得合格与不合格的机会相等,且互不影响.现有

(Ⅰ)求
(Ⅱ)求

正确答案
解析
解析已在路上飞奔,马上就到!