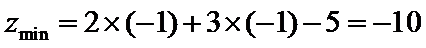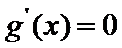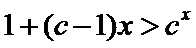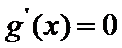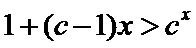- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合

正确答案
解析
由补集的概念,得
考查方向
解题思路
求补集的运算和并的运算即可
易错点
对补集的运算和并的运算出现错误
知识点
2.若

正确答案
解析

考查方向
解题思路
由
易错点
对复数的运算;2、共轭复数;3、复数的模理解出现错误、计算错误
知识点
3.已知向量

正确答案
解析
由题意,得

考查方向
解题思路
由题意,得
易错点
对向量夹角公式理解出现错误、计算错误
知识点
4.某旅游城市为向游客介绍本地的气温情况,绘制了一年中月平均最高气温和平均最低气温的雷达图。图中A点表示十月

正确答案
解析
由图可知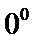
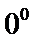
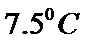
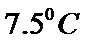
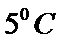
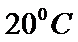
考查方向
解题思路
利用排除法求出即可
易错点
对平均数和统计图理解出现错误、计算错误
知识点
8.执行下图的程序框图,如果输入的a=4,b=6,那么输出的n=
正确答案
解析
第一次循环,得a=2,b=4,a=6,s=6,n=1;第二次循环,得a=-2,b=6,a=4,s=10,n=2;第三次循环,得a=2,b=4,a=6,s=16,n=3;第四次循环,得a=-2,b=6,a=4,s=20>16,n=4,退出循环,输出n=4,故选B
考查方向
解题思路
第一次循环,得a=2,b=4,a=6,s=6,n=1;第二次循环,得a=-2,b=6,a=4,s=10,n=2;第三次循环,得a=2,b=4,a=6,s=16,n=3;第四次循环,得a=-2,b=6,a=4,s=20>16,n=4,退出循环,输出n=4
易错点
对程序框图理解出现错误、计算错误
知识点
9.在


正确答案
解析
设






考查方向
解题思路
由正弦定理,知

易错点
对正弦定理理解出现错误、计算错误
知识点
5.小敏打开计算机时,忘记了开机密码的前两位,只记得第一位是
正确答案
解析
开机密码的可能有



考查方向
解题思路
开机密码的可能有


易错点
对古典概型理解出现错误、计算错误
知识点
6.若

正确答案
解析
考查方向
解题思路
求出
易错点
对同角三角函数间的基本关系和二倍角理解出现错误、计算错误
知识点
7.已知
正确答案
解析
因为





考查方向
解题思路
由函数

易错点
对幂函数的单调性理解出现错误、计算错误
知识点
10.如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为
正确答案
解析
由三视图该几何体是以侧视图为底面的斜四棱柱,所以该几何体的表面积

考查方向
解题思路
三视图该几何体是以侧视图为底面的斜四棱柱,该几何体的表面积即可求出
易错点
对空间几何体的三视图及表面积理解出现错误、计算错误
知识点
11. 在封闭的直三棱柱




正确答案
解析
要使球的体积V最大,必须球的半径R最大,由题意知球的与直三棱柱的上下底面都相切时,球的半径的取得最大值

考查方向
解题思路
要使球的体积V最大,必须球的半径R最大,由题意知球的与直三棱柱的上下底面都相切时,球的半径的取得最大值
易错点
对三棱柱的内切球和球的体积理解出现错误、计算错误
知识点
12.已知O为坐标原点,F是椭圆C: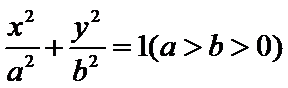
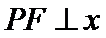
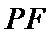
正确答案
解析
由题意设直线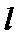
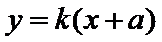
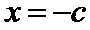
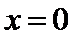
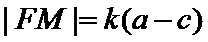
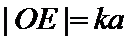
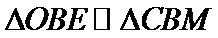
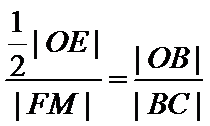
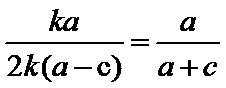
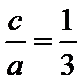
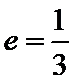
考查方向
解题思路
由题意设直线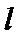
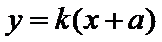
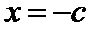
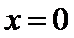
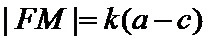
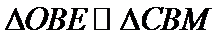
易错点
对椭圆方程与几何性质理解出现错误、计算错误
知识点
13.若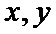
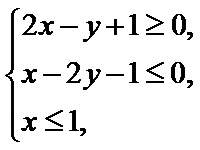
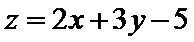
正确答案
解析
作出不等式组满足的平面区域,当目标函数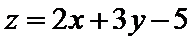
考查方向
解题思路
作出不等式组满足的平面区域,当目标函数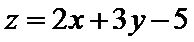
易错点
对简单的线性规划问题理解出现错误、计算错误
知识点
14.函数

正确答案
解析
因为



考查方向
解题思路
因为

易错点
对三角函数图象的平移变换和两角差的正弦函数理解出现错误、计算错误
知识点
16.已知




正确答案
解析
当








考查方向
解题思路
由当





易错点
对函数的奇偶性、解析式、导数的几何意义理解出现错误、计算错误
知识点
15.已知直线








正确答案
4
解析
由


从而可得

考查方向
解题思路
由

易错点
对直线与圆的位置关系理解出现错误、计算错误
知识点
已知各项都为正数的数列


17.求
18.求
正确答案
(Ⅰ)
解析
(Ⅰ)由题意得
考查方向
解题思路
(Ⅰ)将



易错点
对数列的递推公式;等
正确答案
(Ⅱ)
解析
(II)由
由于
故

考查方向
解题思路
(Ⅱ)将已知的递推公式


易错点
对数列的递推公式;等
下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图
19.由折线图看出,可用线
20.建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:


参考公式:相关系数
回归方程
正确答案
(Ⅰ)





解析
(I)由折线图中数据和附注中参考数据得



因为y与t的相关系数近似为0.99,说明y与t的线性相关程度相当高,从而可以用线性回归模型拟合y与t的关系
考查方向
解题思路
(I)根据相关系数r公式求出相关数据后,然后代入公式即可求得r的值,最后根据其值大小回答即可;
易错点
对线性相关与线性回归方程的求法与应用理解出现错误、计算错误
正确答案
(Ⅱ)1.82亿吨
解析
(Ⅱ)由


所以,

将2016年对应的

所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨.
考查方向
解题思路
(II)利用最小乘法的原理提供的回归方程,准确求得相关数据即可建立y关于t的回归方程,然后作预测。
易错点
对线性相关与线性回归方程的求法与应用理解出现错误、计算错误
如图,四棱锥










21.证明

22.求四面体
正确答案
(Ⅰ)(I)由已知,得



于是


解析
(I)由已知,得






来源:学科网]
考查方向
解题思路
(I)取PB的中点T,证明AMNT为平行四边形,可得到
易错点
对直线与平面间的平行与垂直关系和三棱锥的体积理解出现错误、计算错误
正确答案
解析
因为



所以

取





由




所以四面体
考查方向
解题思路
(I)取PB的中点T,证明AMNT为平行四边形,可得到

易错点
对直线与平面间的平行与垂直关系和三棱锥的体积理解出现错误、计算错误
已知抛物线








23.若




24.若


正确答案
(Ⅰ)由题设









设AR的斜率为

所以
解析
由题设









设AR的斜率为

所以
考查方向
解题思路
(I)设出与x轴垂直的两条直线,然后得出A,B,P,Q,R的坐标,然后通过证明直线AR与直线FQ的斜率相等即可证明结果了;
易错点
对抛物线定义与几何性质、直线与抛物线位置关系和轨迹求法理解出现错误、计算错误
正确答案
(Ⅱ)
解析
(Ⅱ)设


则
由题设可得


设满足条件的

当



而

当



考查方向
解题思路
(II)设直线l与x轴的交点坐标


易错点
对抛物线定义与几何性质、直线与抛物线位置关系和轨迹求法理解出现错误、计算错误
设函数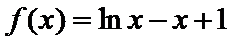
25.讨论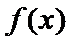
26.证明当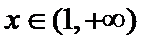
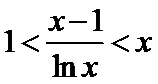
27.设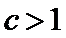
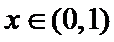
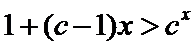
正确答案
(Ⅰ)当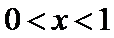
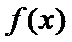
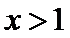
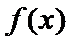
解析
(I)由题设,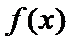
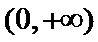
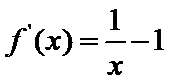
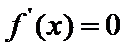
当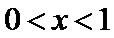
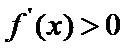
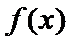
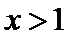
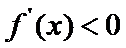
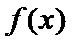
考查方向
解题思路
(I)首先求出导函数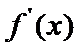
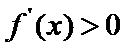
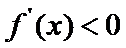
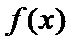
易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
正确答案
(Ⅱ)(II)由(I)知,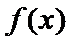
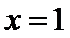
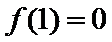
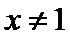
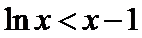
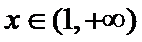
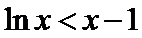
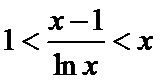
解析
(II)由(I)知,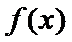
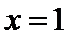
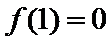
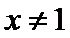
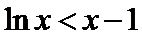
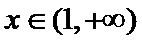
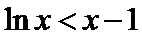
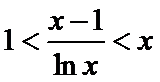
考查方向
解题思路
(II)左端等式可利用(I)的结论证明,右端将左端的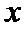

易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
正确答案
(Ⅲ)(III)由题设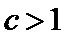
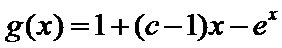
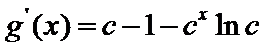
解得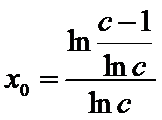
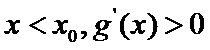
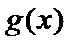
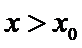
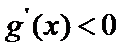
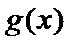
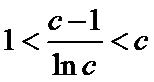
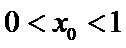
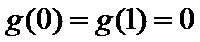
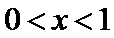
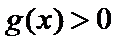
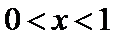
解析
(III)由题设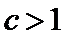
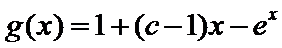
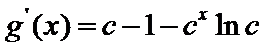
解得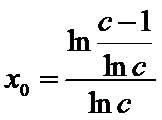
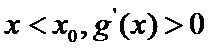
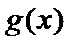
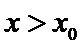
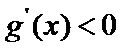
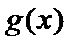
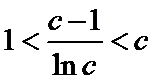
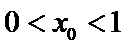
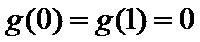
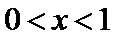
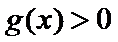
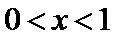
考查方向
解题思路
变形所证不等式构造新函数,然后通过利用导数研究函数的单调性来处理
易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
考生在以下3题中任选一道作答,并用2B铅笔将答题卡上所选的题目对应的题号右侧方框涂黑,按所涂题号进行评分;多涂、多答,按所涂的首题进行评分

如图,⊙O中




选修4-4:坐标系与参数方程(请回答30、31题)
在直角坐标系





选修4-5:不等式选讲(请回答32、33题)
已知函数
28.若

29.若



30.写出

31.设点P在

32.当a=2时,求不等式
33.设函数



正确答案
(Ⅰ)
解析
(I)连接PB、BC,则
因为AP=BP,所以

又
考查方向
解题思路
(I)根据条件可证



易错点
对圆周角定理、三角形内角和定理、垂直平分线定理、四点共圆理解出现错误、计算错误
正确答案
(Ⅱ)(II)因为

解析
(II)因为

考查方向
解题思路
(II)由(I)的证明可知C、E、F、D四点共圆,然后根据用线段的垂直平分线知G为四边形CEFD的外接圆圆心,则可知G在线段CD的垂直平分线上,由此可证明结果
易错点
对圆周角定理、三角形内角和定理、垂直平分线定理、四点共圆理解出现错误、计算错误
正确答案
(Ⅰ)



解析
利用同角三角函数基本关系中的平方关系化曲线




考查方向
解题思路
(I)利用同角三角函数基本关系中的平方关系化曲线

易错点
对椭圆的参数方程、直线的极坐标方程理解出现错误、计算错误
正确答案
(Ⅱ)
解析
(II)利用参数方程表示出点P的坐标,然后利用点到直线的距离公式建立三角函数的表达式,然后求出最值与相应的点P的坐标即可
由已知,设P的直角坐标为



当且仅当


考查方向
解题思路
(II)利用参数方程表示出点P的坐标,然后利用点到直线的距离公式建立三角函数的表达式,然后求出最值与相应的点P的坐标即可
易错点
对椭圆的参数方程、直线的极坐标方程理解出现错误、计算错误
正确答案
(Ⅰ)
解析
(Ⅰ)当

解不等式

因此,
考查方向
解题思路
(Ⅰ)利用等价不等式
易错点
对绝对值不等式的解法、三角形绝对值不等式的应用理解出现错误、计算错误
正确答案
(Ⅱ)
解析
(Ⅱ)当

当
所以当

当

当


所以
考查方向
解题思路
(Ⅱ)根据条件可首先将问题转化求解

易错点
对绝对值不等式的解法、三角形绝对值不等式的应用理解出现错误、计算错误