- 真题试卷
- 模拟试卷
- 预测试卷
6.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.下列函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知锐角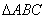
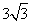
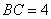
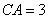
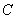
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.平面内




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设偶函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.集合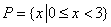
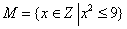
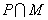
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设向量

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.实数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.函数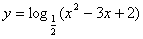
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.下列四个命题:
①函数
②命题





③函数
④函数

其中正确命题的序号是____________。(把你认为正确的序号都填上)。
正确答案
①④
解析
解析已在路上飞奔,马上就到!
知识点
17.已知向量




正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
16.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知:向量




(1)若


(2)若



正确答案
(1)∵

①若





②若





(2)∵

∴ 


∴|






∴
解析
解析已在路上飞奔,马上就到!
知识点
20.已知:函数



(1)求:
(2)当

正确答案
(1)由最高点为


由点

所以
又


(2)因为
所以当
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知:函数



(1)求:
(2)求:
正确答案
(Ⅰ)由题意得
因此
因为函数

即对任意实数x,有
从而3a+1=0,b=0,解得
因此

(Ⅱ)由(Ⅰ)知

令


当


从而


当



由前面讨论知,

而


因此


解析
解析已在路上飞奔,马上就到!
知识点
22.已知:向量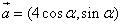
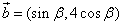
(1)若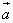
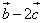
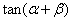
(2)求:
(3)若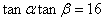
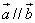
正确答案
(1)由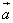
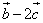
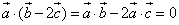
即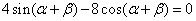
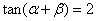
(2)
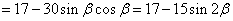
最大值为32,所以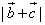
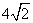
(3)由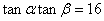
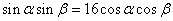
即 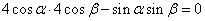
所以
解析
解析已在路上飞奔,马上就到!
知识点
23.已知:函数


求:实数
正确答案
解:依据题意得

即

当


所以


解析
解析已在路上飞奔,马上就到!