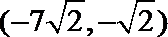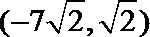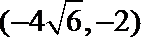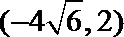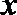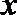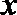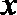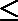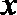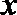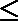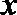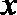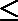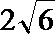- 真题试卷
- 模拟试卷
- 预测试卷
1.复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图象是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.将圆x2+y2 -2x-4y+1=0平分的直线是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.在平面直角坐标系中,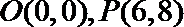
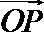
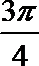
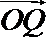
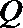
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.样本(







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.命题“存在实数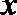
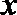
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.一个几何体的三视图形状都相同,大小均相等,那么这个几何体不可以是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.下列命题正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知F1、F2为双曲线C:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设a>0,b>0,下列选项正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 如图是用模拟方法估计圆周率

入( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.若曲线



正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
16.对于实数







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.公比为2的等比数列{
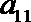
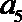
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
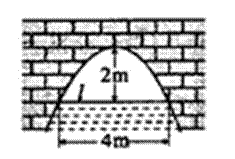
14.右图是抛物线形拱桥,当水面在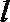
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
(Ⅰ)试估计厨余垃圾投放正确的概率;
(Ⅱ)试估计生活垃圾投放错误额概率;
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为








正确答案
(Ⅰ)由题意可知:
(Ⅱ)由题意可知:
(Ⅲ)由题意可知:
因此当



解析
解析已在路上飞奔,马上就到!
知识点
20. 在平面直角坐标系






(Ⅰ)求椭圆
(Ⅱ)设直线




正确答案
(Ⅰ)因为椭圆


点



所以
所以椭圆

(Ⅱ)直线





因为直线


整理得



因为直线


整理得
综合①②,解得

所以直线


解析
解析已在路上飞奔,马上就到!
知识点
17.已知
(Ⅰ)求数列
(Ⅱ)记




正确答案
(Ⅰ)设数列

解得
所以
(Ⅱ)由(Ⅰ)可得
因

从而
解得


解析
解析已在路上飞奔,马上就到!
知识点
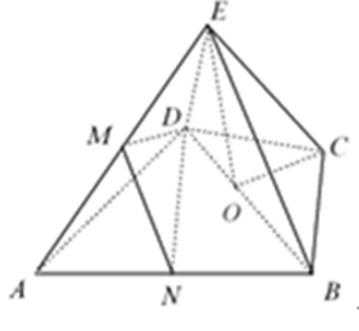
19.如图,几何体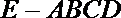
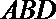
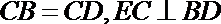
(Ⅰ)求证: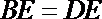
(Ⅱ)若∠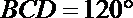
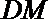
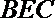
正确答案
(I)设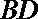
则由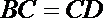
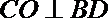
又已知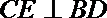
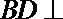
所以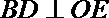
所以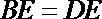
(II)取AB中点N,连接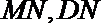
∵M是AE的中点,∴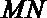

∵△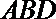
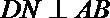
由∠BCD=120°知,∠CBD=30°,所以∠ABC=60°+30°=90°,即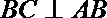
所以ND∥BC,
所以平面MND∥平面BEC,故DM∥平面BEC.
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(Ⅰ)求k的值;
(Ⅱ)求
(Ⅲ)设



正确答案
(I)
由已知,

(II)由(I)知,
设



由



当


综上可知,


(III)由(II)可知,当




当



设


当



所以当


所以
综上,对任意

解析
解析已在路上飞奔,马上就到!
知识点
从22、23、24题中任选一题作答。
22.选修4-1:几何证明选讲
如图,圆O和圆



证明:(I)
(II)
23. 选修4-4:坐标系与参数方程
在直角坐标系


(I)在以



(II)求圆

24. 选修4-5:不等式选讲
已知

(I)求
(II)若

正确答案
22.证明:(I)由



所以

从而
即
(II)由


又

从而

综合(I)的结论,
23.(I)圆



解



(II)由


故圆

24.(I)由



当
当


(II)记

所以

解析
解析已在路上飞奔,马上就到!