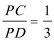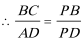- 真题试卷
- 模拟试卷
- 预测试卷
3.已知函数
正确答案
解析







知识点
4.复数



正确答案
解析




知识点
5.下列四类函数中,具有性质“对任意的



正确答案
解析
对于A选项,取

















知识点
7.等差数列





正确答案
解析
设等差数列













知识点
2.过点

正确答案
解析
根据垂直直线系的直线的方程的特点,不妨设所求直线的方程为





知识点
6.“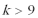
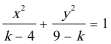
正确答案
解析
方程“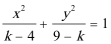
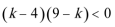
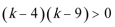
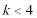
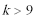
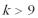
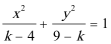
知识点
9.在




正确答案
解析











知识点
10.半径不等的两定圆







正确答案
解析
设定圆












若定圆











若定圆











知识点
1.设全集为



正确答案
解析




知识点
8.直线

正确答案
解析
将圆的方程化为标准式得






知识点
13.椭圆



正确答案

解析
双曲线的离心率
知识点
11.函数



正确答案

解析
由反函数的定义知,函数







知识点
选做题(14、15题,只能从中选做一题)
14.在同一平面坐标系中,经过伸缩变换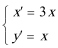
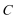
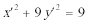
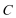
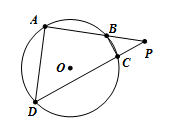
15.如图,四边形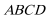
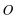
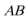
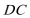
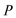
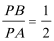
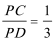
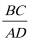
正确答案
14.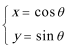
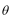
15.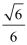
解析
14.将
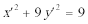
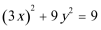
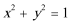
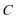
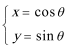
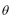
15.由于四边形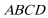
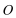
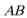
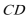
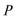
则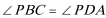
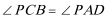
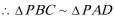
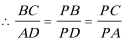
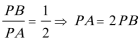
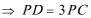
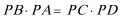
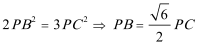
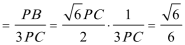
知识点
12.已知

正确答案

解析
由于







知识点
17.已知函数

(1)当


(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.椭圆以坐标轴为对称轴,且经过点



(1)求圆心在线段
(2)在椭圆位于第一象限的弧


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知二次函数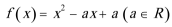
①不等式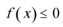
②在定义域内存在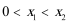
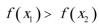
数列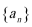
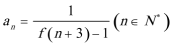
(1)求函数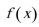
(2)求数列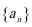
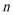
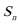
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在锐角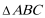
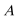
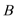

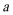
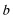
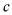
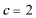

(1)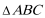
(2)当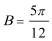
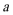
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数

(1)求
(2)若
(Ⅰ)证明:当


(Ⅱ)证明不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图示:已知抛物线














(1)当点


(2)证明:
正确答案
解析
解析已在路上飞奔,马上就到!