- 真题试卷
- 模拟试卷
- 预测试卷
10.设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 在复平面内,复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.给定命题p:函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知等边


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.等差数列中,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.如图所示的程序框图输出的所有点都在函数( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.把边长为的正方形ABCD沿对角线BD折起,连结AC,得到三棱锥C-ABD,其正视图、俯视图均为全等的等腰直角三角形(如图所示),则其侧视图的面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数

(Ⅰ) 当a=5时,求函数

(Ⅱ) 求
(Ⅲ) 若存在两不等实根

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
(1)判断是否有99.5%的把握认为喜欢“人文景观”景点与年龄有关?
(2)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率.
下面的临界值表供参考:
(参考公式: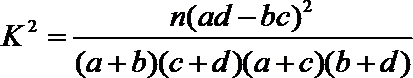
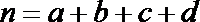
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
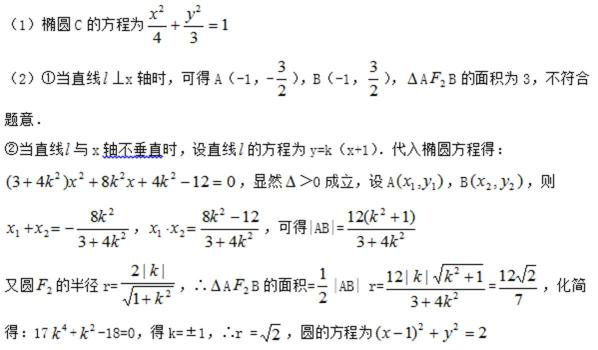
20. 已知椭圆C的对称中心为原点O,焦点在x轴上,左右焦点分别为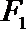
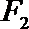
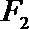

(1)求椭圆C的方程;
(2)过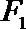
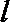
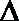
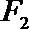
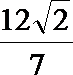
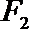
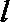
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知函数

(1)求函数

(2)已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请在22,23,24题中任选一题作答。
22.选修4—1:几何证明选讲
如图,已知⊙O的半径为1,MN是⊙O的直径,过M点作⊙O的切线AM,C是AM的中点,AN交⊙O于B点,若四边形BCON是平行四边形;
(Ⅰ)求AM的长;
(Ⅱ)求
23. 已知曲线C的极坐标方程是


(Ⅰ)将曲线C的极坐标方程化为直角坐标方程,将直线
(Ⅱ)若直线l与曲线C相交于A、B两点,且
24. 已知函数
(Ⅰ)若不等式

(Ⅱ)在(Ⅰ)的条件下,若存在实数


正确答案
22.
23.
24.
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,在四棱锥






(1)求证:

(2)求四面体
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在面积为S的矩形ABCD内随机取一点P,则△PBC的面积小于
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知数列

正确答案
91
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知点P的坐标

正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
15.已知三角形




正确答案
解析
解析已在路上飞奔,马上就到!