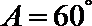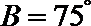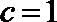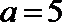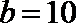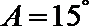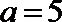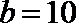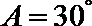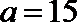- 真题试卷
- 模拟试卷
- 预测试卷
15.根据以下各组条件解三角形, 解不唯一的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.将正方体其余6个顶点标上字母, 使其成为正方体
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.对于数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设平面向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.在数列







正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
14.设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.平面上的点


正确答案
(4,-3)
解析
解析已在路上飞奔,马上就到!
知识点
5.在下边所示流程图中, 若输入的


正确答案
7
解析
解析已在路上飞奔,马上就到!
知识点
7.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知命题“



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设




正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
4.若复数


正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
6.设



正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
9.设全集


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设



正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
20.某学生解下
【题目】有一块铁皮零件, 它的形状是由边长为








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数

(1) 设

(2) 设


(3) 设




正确答案





解析
解析已在路上飞奔,马上就到!
知识点
19.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1) 写出
(2) 若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.可以证明, 对任意的

(1) 设由三项组成的数列


(2) 设数列







(3) 是否存在满足(2)中条




正确答案



解析
解析已在路上飞奔,马上就到!