- 真题试卷
- 模拟试卷
- 预测试卷
1. 设i是虚数单位,a∈R,若
正确答案
解析
略
知识点
7. 如图程序框图中,若输入m=4,n=10,则输出a,i的值分别是( )
正确答案
解析
略
知识点
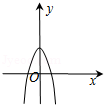
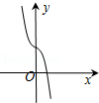
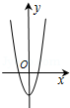
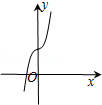
9.函数y=4cosx﹣e|x|(e为自然对数的底数)的图象可能是( )
正确答案
解析
略
知识点
3.若某公司从五位大学毕业生甲、乙、丙、丁、戌中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率为( )
正确答案
解析
略
知识点
5.若a=20.5,b=ln2,c=0.5e(e是自然对数的底),则( )
正确答案
解析
略
知识点
5. 已知点 M(x,y)的坐标满足

正确答案
解析
略
知识点
6. 某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x的值是( )
正确答案
解析
略
知识点
2. 已知集合A={x|x2≥1},B={x|y=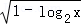
正确答案
解析
略
知识点
8. 已知P(x,y)是直线kx+y+4=0(k>0)上一动点,PA是圆C:x2+y2﹣2y=0的一条切线,A是切点,若PA长度最小值为2,则k的值为( )
正确答案
解析
略
知识点
10. 偶函数f(x)满足f(x﹣1)=f(x+1),且在x∈[0,1]时,f(x)=x2,则关于x的方程f(x)=
正确答案
解析
略
知识点
11. 函数
正确答案
{x|x>2且x≠3}
解析
略
知识点
13. 已知x>0,y>0,且2x+y=1,则

正确答案
8
解析
略
知识点
12. 平面向量





正确答案
2
解析
略
知识点
14. 已知抛物线y2=2px的焦点F与双曲线


正确答案
32
解析
略
知识点
15. 若X是一个集合,τ是一个以X的某些子集为元素的集合,且满足:
①X属于τ,∅属于τ;
②τ中任意多个元素的并集属于τ;
③τ中任意多个元素的交集属于τ.则称τ是集合X上的一个拓扑.已知集合X={a,b,c},对于下面给出的四个集合τ:
①τ={∅,{a},{c},{a,b,c}};
②τ={∅,{b},{c},{b,c},{a,b,c}};
③τ={∅,{a},{a,b},{a,c}};
④τ={∅,{a,c},{b,c},{c},{a,b,c}}.
其中是集合X上的拓扑的集合τ的序号是 ().
正确答案
②④
解析
略
知识点
20. 椭圆

(1)求椭圆C的方程;
(2)若直线l:y=kx+t与椭圆C交于M,N两点,以线段OM,ON为邻边作平行四边形OMGN
其中G在椭圆C上,当
正确答案
见解析
解析
解:(1)∵直线l:x+my=

∴椭圆的右焦点F2

∴△F1PQ的周长为8,∴4a=8,解得a=2,
∴b2=a2﹣c2=1,
∴椭圆C的方程为
(2)联立
由△=64k2t2﹣4(1+4k2)(4t2﹣4)>0,可得4k2+1>t2.
设M(x1,y1),N(x2,y2),G(x0,y0),则
∵四边形OMGN是平行四边形,∴

可得G
∵G在椭圆C上,∴

∴4t2=4k2+1,
∴|OG|2=




∵

∴
∴|OG|的取值范围是
知识点
16. △ABC中,A,B,C所对的边分别为a,b,c,
(1)求A,B,C;
(2)若S△ABC=3+
正确答案
见解析
解析
解:(1)∵

∴sinCcosA+sinCcosB=cosCsinA+cosCsinB,
即 sinCcosA﹣cosCsinA=cosCsinB﹣sinCcosB,
得 sin(C﹣A)=sin(B﹣C).
∴C﹣A=B﹣C,或C﹣A=π﹣(B﹣C)(不成立).
即 2C=A+B,得
∴
∵
则

∴
(2)∵
又∵
即 
∴
知识点
21. 已知函数f(x)=x﹣alnx(a∈R).
(1)当a=2时,求曲线f(x)在x=1处的切线方程;
(2)设函数h(x)=f(x)+
(3)若g(x)=﹣
正确答案
见解析
解析
解:(1)当a=2时,f(x)=x﹣2lnx,f(1)=1,切点(1,1),
∴
∴曲线f(x)在点(1,1)处的切线方程为:y﹣1=﹣(x﹣1),即x+y﹣2=0.
(2)

①当a+1>0,即a>﹣1时,令h′(x)>0,
∵x>0,∴x>1+a
令h′(x)<0,∵x>0,∴0<x<1+a.
②当a+1≤0,即a≤﹣1时,h′(x)>0恒成立,
综上:当a>﹣1时,h(x)在(0,a+1)上单调递减,在(a+1,+∞)上单调递增.
当a≤﹣1时,h(x)在(0,+∞)上单调递增.
(3)由题意可知,在[1,e]上存在一点x0,使得f(x0)≤g(x0)成立,
即在[1,e]上存在一点x0,使得h(x0)≤0,
即函数
由第(2)问,①当a+1≥e,即a≥e﹣1时,h(x)在[1,e]上单调递减,
∴

∵

②当a+1≤1,即a≤0时,h(x)在[1,e]上单调递增,
∴[h(x)]min=h(1)=1+1+a≤0,
∴a≤﹣2,
③当1<a+1<e,即0<a<e﹣1时,∴[h(x)]min=h(1+a)=2+a﹣aln(1+a)≤0,
∵0<ln(1+a)<1,∴0<aln(1+a)<a,∴h(1+a)>2
此时不存在x0使h(x0)≤0成立.
综上可得所求a的范围是:
知识点
19. 已知数列{an}的前n项和为Sn,an.Sn满足(t﹣1)Sn=t(an﹣2)(t为常数,t≠0且t≠1).
(1)求数列{an}的通项公式;
(2)设bn=(﹣an)•log3(1﹣Sn),当t=
正确答案
见解析
解析
解:(1)由(t﹣1)Sn=t(an﹣2),及(t﹣1)Sn+1=t(an+1﹣2),作差得an+1=tan,
即数列{an}成等比数列,
当n=1时,(t﹣1)S1=t(a1﹣2),解得a1=2t,故
(2)当





作差得
所以
知识点
17. 某商区停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过1小时收费6元,超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过4小时.
(1)若甲停车1小时以上且不超过2小时的概率为

(2)若每人停车的时长在每个时段的可能性相同,求甲、乙二人停车付费之和为36元的概率.
正确答案
见解析
解析
解:(1)设“甲临时停车付费恰为6元”为事件A,
则 
所以甲临时停车付费恰为6元的概率是
(2)设甲停车付费a元,乙停车付费b元,其中a,b=6,14,22,30.
则甲、乙二人的停车费用构成的基本事件空间为:(6,6),(6,14),(6,22),(6,30),(14,6),(14,14),(14,22),(14,30),(22,6),(22,14),(22,22),(22,30),(30,6),(30,14),(30,22),(30,30),共16种情形.
其中,(6,30),(14,22),(22,14),(30,6)这4种情形符合题意.
故“甲、乙二人停车付费之和为36元”的概率为
知识点
18. 如图正方形ABCD的边长为ABCD的边长为2

(1)求证:AE∥平面BCF;
(2)求证CF⊥平面AEF.
正确答案
见解析
解析
(1)证明:取BC中点H,连结OH,则OH∥BD,
又四边形ABCD为正方形,∴AC⊥BD,
∴OH⊥AC,∴以O为原点,建立如图所示的直角坐标系,
则A(3,0,0),E(1,﹣2,0),C(﹣1,0,0),
D(1,﹣2,0),F(0,0,





设平面BCF的法向量为
则



又四边形BDEF为平行四边形,
∴


∴






∴




∴AE
(2)证明:

∴



∴



又AE∩AF=A,∴CF⊥平面AEF.