- 真题试卷
- 模拟试卷
- 预测试卷
5.如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该几何体的各个面中最大面的面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.命题“若对任意的 

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若实数x,y满足

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数f(x)的部分图象如图所示,则下列关于f(x)的表达式中正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知F1、F2分别是双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.定义在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.在如图所示的方格柢中,向量a,b,c的起点和终点均在格点(小正方形顶点)上,若c与xa+yb(x,y为非零实数)共线,则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.等比数列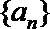

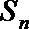
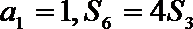
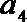
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
14.直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知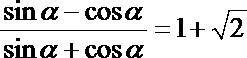
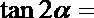
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
15.已知集合



①
②
③
④
其中是“垂直对点集”的序号是( )
正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求函数
(2)若


正确答案
(1)解:


∴ 函数

(2)
∵

∴ 
∴ 
∵ 
∴ 
∴ 
∴

解析
解析已在路上飞奔,马上就到!
知识点
17.如图,茎叶图记录了甲组3名同学寒假假期中去图书馆A学习的次数和乙组4名同学寒假假期中去图书馆B学习的次数.乙组记录中有一个数据模糊.,无法确认,在图中以x表示.
甲组 乙组
(1)如果x=7,求乙组同学去图书馆学习次数的平均数和方差;
(2)如果x=9,从学习次数大于8的学生中选两名同学,求选出的两名同学恰好分别在两个图书馆学习且学习的次数和大于20的概率.
正确答案
答案已在路上飞奔,马上就到!
解析
(1)
(2)设学习次数大于8的同学共有6名,设为a、b、c、d、e、f,从中任选两名,则




设A=“两名同学恰好分别在两个图书馆学习且学习的次数和大于20”
则A={(9,12),(9,12)(11,12),(12,9)(12,12)}共5种.
所以
知识点
19.已知数列






(1)求
(2)求数列
(3)是否存在正整数




正确答案
(1)解:∵

∴
∴ 
∴ 
(2)解法1:由

∴ 数列


∴ 
∴ 
当

而
∴ 
解法2:由

∴
当

①

∴
∴
∴ 数列


∴ 
而
∴ 
(3)解:由(2)知

假设存在正整数



则
即
∵ 
∴
得

解得


∴ 不存在正整数



解析
解析已在路上飞奔,马上就到!
知识点
20.设点




(1)求椭圆
(2)设过右焦点






正确答案
(1)解:设

所以 

则椭圆方程为 
又点
所以 

故椭圆方程为 
(2)解:由题意,直线

设直线

由 

得 
由题意,可知


所以直线



所以

即 
所以当



解析
解析已在路上飞奔,马上就到!
知识点
18.在边长为












(1)求证:

(2)求四棱锥
正确答案
(1)证明:∵点



∴ 

∵ 菱形
∴ 
∴ 
∴ 

∵ 




∴ 

∴ 

(2)解:设

∵ 
∴ △
∴ 



在R t△

在△

∴ 
∵ 





∴ 

梯形

∴ 四棱锥

解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)当a = 1,b = 2时,求函数y = f (x)-g (x)的图象在点(1,f (1))处的切线方程;
(2)若2a = 1-b(b > 1),讨论函数y = f (x)-g (x)的单调性;
(3)若对任意的b∈[-2,-1],均存在x∈(1,e)使得f (x) < g (x),求实数a的取值范围
正确答案
(1)令
当a = 1,b = 2时,

∴函数y = f (x)-g (x)的图象在点(1,f (1))处的切线方程为y-3 = 3(x-1)
即3x-y = 0
(2)解:
当


当
当

(3)解:依题意, b∈[-2,-1],x∈(1,e)使得f (x) < g (x)成立
即b∈[-2,-1],x∈(1,e),F(x) < 0成立
即b∈[-2,-1],

令

∵b∈[-2,-1],x∈(1,e),∴-2x + 1≤bx + 1≤-x + 1 < 0,-2ln x < 0
因此
又G(1) =-b,∴G(x)max =-b∈[1,2]
∴a<1,即实数a的取值范围是(-∞,1)
解析
解析已在路上飞奔,马上就到!






























































