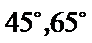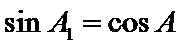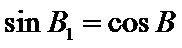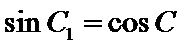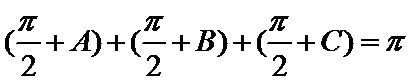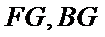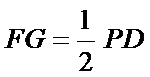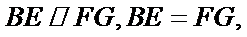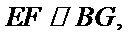- 真题试卷
- 模拟试卷
- 预测试卷
8.已知点







正确答案
解析
因为点









考查方向
本题考查的知识点为:
1.中点公式;
2.直线垂直的判定与性质;
3.两点间距离公式.在近几年的各省高考题出现的频率非常高,常圆锥曲线与直线交汇命题.
解题思路
设出线段PA的中点Q的坐标,因直线PA与FQ垂直,可建立方程。
易错点
解方程时易出现错误.
知识点
7. 已知函数
正确答案
解析
显然
因为当

令



因为函数






故选D.
考查方向
本题考查的知识点有:
1.三角函数的奇偶性;
2.三角函数的单调性;
3.三角函数的值域.
解题思路
常规方法是逐项检验,但如果能发现选项D明显正确,则可避免验证其他三项,以节约时间.
易错点
代数方法易出错,建议画图,直观上判断.
知识点
1. 复数
正确答案
解析


考查方向
本题考查了复数的计算能力,在近几年的各省高考题出现的频率非常高,常单独命题.
解题思路
直接按照平方差公式计算即可.
易错点
注意
知识点
3. 如图, 正方形




正确答案
解析
因为


考查方向
本题考查了平面向量的三角形法则,在近几年的各省高考题出现的频率较低.
解题思路
利用基向量

易错点
使用加法公式

知识点
4. 如图,在边长为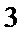
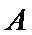
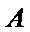
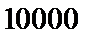
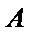
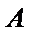
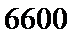
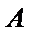
正确答案
解析
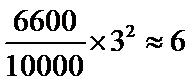
考查方向
本题考查了蒙特卡洛方法.在近几年的各省高考题出现的频率较低.
解题思路
先利用蒙特卡洛方法计算出阴影区域所占的比例,再计算阴影区域的面积.
易错点
审题失误.
知识点
6. 若点


正确答案
解析
由题意知:



考查方向
本题考查了不等式与半平面的关系,在近几年的各省高考题出现的频率较低.
解题思路
点



易错点
审题失误,注意点不在区域内.
知识点
2. 已知数列


正确答案
解析
因为


考查方向
本题考查的知识点为等比数列第二通项公式,在近几年的各省高考题出现的频率较高.
解题思路
先移项,利用等比数列的第二通项公式求出

易错点
不合理变形为
知识点
5. 某程序框图如图所示,执行该程序,如输入的

正确答案
解析
第一次循环:

第二次循环:

第三次循环:



考查方向
本题考查了程序框图的读图能力,在近几年的各省高考题出现的频率非常高.
解题思路
逐步写出循环中各个量的变化,判断条件,直至条件成立.
易错点
循环次数判断错误.
知识点
9.若
正确答案
10
解析



考查方向
本题考查了对数的运算能力.
解题思路
将右侧的常数转化为同底对数.
易错点
对数的运算性质模糊不清致误.
知识点
12. 直线




正确答案
解析
设切点B的横坐标为










考查方向
本题考查了导数的几何意义,在近几年的各省高考题出现的频率较高.
解题思路
设出切点,根据切点与斜率求出直线方程.
易错点
如果由点A与斜率确定直线方程,则该题不易算出.
知识点
13. 已知圆


正确答案
2或6
解析
由勾股定理知,圆心到直线的距离等于
由点到直线的距离知,圆心到直线的距离等于


考查方向
本题考查了圆与直线的相交弦问题.
解题思路
利用不同的计算方法,得到等量关系.
易错点
本题如使用弦长公式求解,会使得问题复杂化.
知识点
14. 已知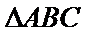
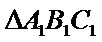
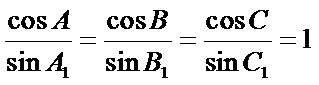
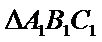
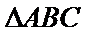
(i) 在满足下述条件的三角形中,存在“友好”三角形的是____:(请写出符合要求的条件的序号)
①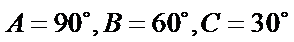
②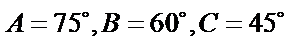
③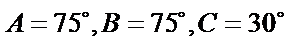
(ii) 若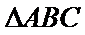
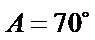
正确答案
②;
解析
(i) ①因为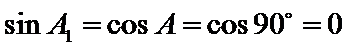
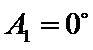
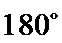
②因为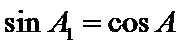
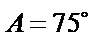
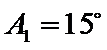
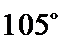
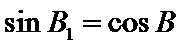
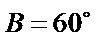
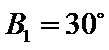
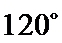
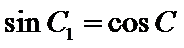
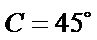
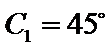
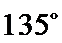

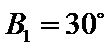
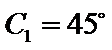
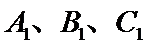
③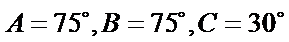
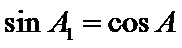
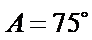
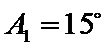
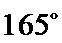
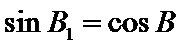
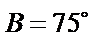
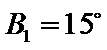
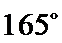
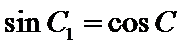
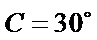
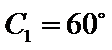
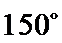
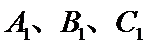
(ii)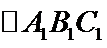
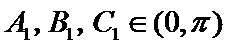
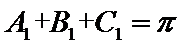
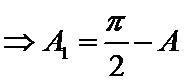
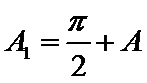
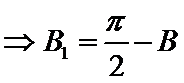
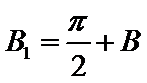

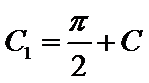
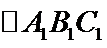
a.三个“-”;
b.三个“+”;
c.两个“-”一个“+”;
d.两个“+”一个“-”.
a.三个“-”;
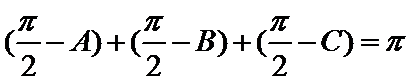
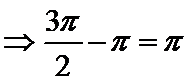
b.三个“+”;
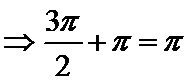
c.两个“-”一个“+”;
不妨设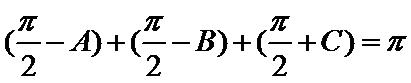
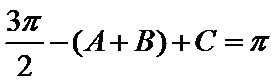
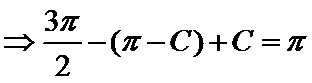
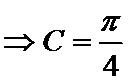
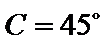
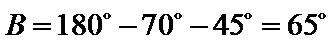
d.两个“+”一个“-”.
不妨设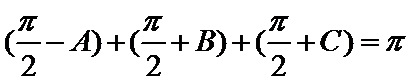

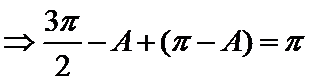
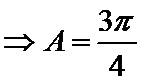
考查方向
本题考查了诱导公式,分类讨论思想,在近几年的各省高考题出现的频率较低.
解题思路
由方程、诱导公式解得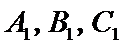
易错点
没有检查三角能不能构成三角形致误.
知识点
10. 已知双曲线


正确答案
2,
解析
双曲线






考查方向
本题考查了双曲线的渐近线、离心率,在近几年的各省高考题出现的频率较高.
解题思路
通过渐近线先求出b的值,再求出离心率.
易错点
注意双曲线中是
知识点
11. 某三棱柱的三视图如图所示,则该三棱柱的体积为
正确答案
4
解析
如图,画出三棱柱,可知体积
考查方向
本题考查了通过三视图还原实物的能力,在近几年的各省高考题出现的频率非常高.
解题思路
由三视图可知三棱柱的一个侧面是水平放置的.
易错点
不能还原出实物图像.
知识点
15. 等差数列




(Ⅰ)求
(Ⅱ)求满足不等式

正确答案
(Ⅰ)
(Ⅱ)
解析
(Ⅰ)设数列

因为

因为


所以
(Ⅱ)因为


所以

解得


考查方向
本题考查了等差数列的通项公式、前n项和公式.在近几年的各省高考题出现的频率非常高.
解题思路
(Ⅰ)将通项公式代入
(Ⅱ)代入求和公式,解不等式即可.
易错点
移项时注意变号.
知识点
16. 已知函数
(Ⅰ)求函数
(Ⅱ)求函数

正确答案
(Ⅰ)
(Ⅱ)
解析
(Ⅰ)因为
所以函数

(Ⅱ)因为
所以

根据函数
当


当


因为
所以函数


考查方向
本题考查了二倍角公式,周期,单调性与最值,在近几年的各省高考题出现的频率非常高.
解题思路
(Ⅰ)化为同角同名函数;
(Ⅱ)利用整体思想.
易错点
在第二问中,注意把
知识点
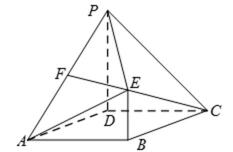
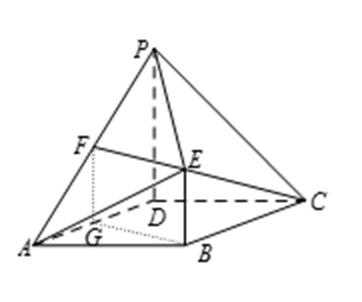
18. 如图,四边形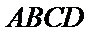
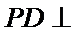
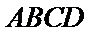
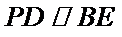
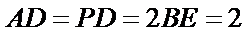
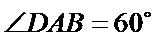
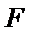
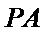
(Ⅰ)求证: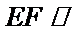
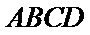
(Ⅱ)求证:平面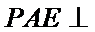
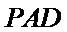
(Ⅲ)求三棱锥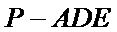
正确答案
(Ⅰ)略;
(Ⅱ)略;
(Ⅲ)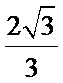
解析
(Ⅰ)取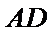
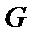
因为点
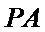
所以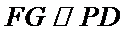
又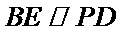
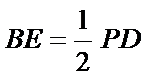
所以
所以四边形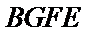
所以
又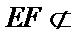
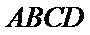
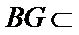
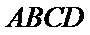
所以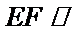
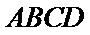
(Ⅱ)连接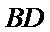
因为四边形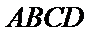
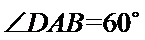

因为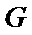
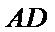
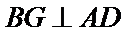
又因为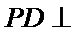
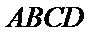
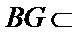
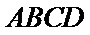
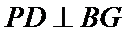
又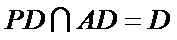
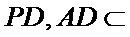
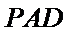
所以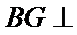
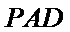
又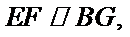
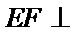
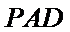
又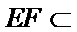
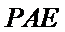
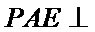
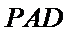
法二:因为四边形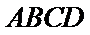
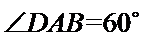
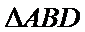
因为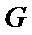
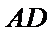
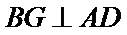
又因为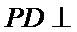
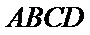
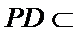
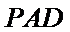
所以平面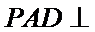
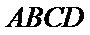
又平面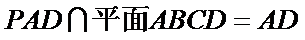
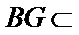
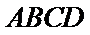
所以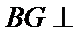
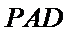
又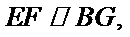
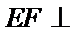
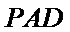
又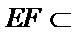
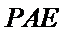
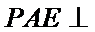

(Ⅲ)因为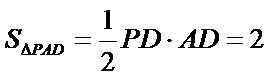
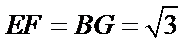
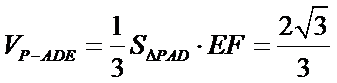
考查方向
本题考查了线面平行,面面垂直的证明,体积的求法,在近几年的各省高考题出现的频率非常高.
解题思路
(Ⅰ)借助于平行四边形,得到线线平行,进而得到线面平行;
(Ⅱ)利用面面垂直的判定定理;
易错点
定理记忆不清致误.
知识点
19. 已知函数
(Ⅰ)当

(Ⅱ)若关于


正确答案
(Ⅰ)




(Ⅱ)

解析
(Ⅰ)函数


当

令

所以

所以





(Ⅱ)因为关于

令

所以
令

当




而

所以函数
当


所以

当


当



综上,当



法二:
因为关于

所以问题等价于方程
令

令
当


所以函数



所以函数
当


所以函数


当


当

所以函数
综上,当



法三:因为关于

所以问题等价于方程
设函数

令



所以函数


又当


所以函数

所以当


所以
考查方向
本题考查了利用导数求函数的单调性与极值,在近几年的各省高考题出现的频率非常高.
解题思路
(Ⅰ)求出函数

(Ⅱ)将方程解的问题转换为函数存在零点问题.
易错点
未注意到函数的定义域致误.
知识点
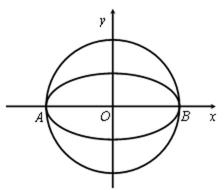
20.如图,椭圆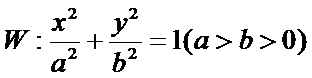
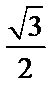
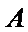
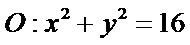
(Ⅰ)求椭圆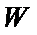
(Ⅱ)直线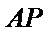
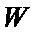
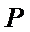

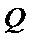
(i)当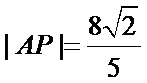
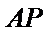
(ii)是否存在直线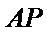
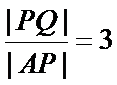
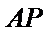
说明理由.
正确答案
(Ⅰ)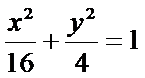
(Ⅱ)(i)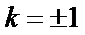
(ii)不存在直线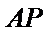
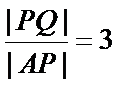
解析
(Ⅰ)
因为椭圆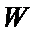

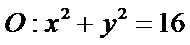
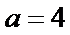
又离心率为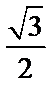
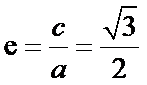
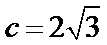
所以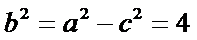
所以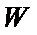
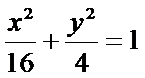
(Ⅱ)(i)
法一:设点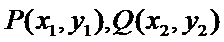
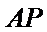
设直线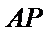
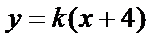
与椭圆方程联立得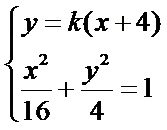
化简得到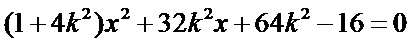
因为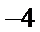

所以
由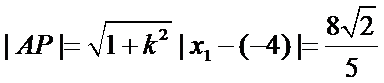
代入得到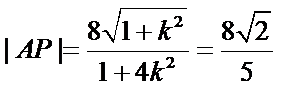
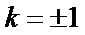
所以直线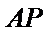
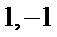
(ii)因为圆心到直线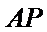
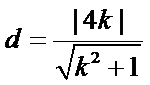
所以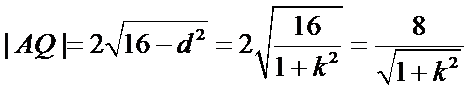
因为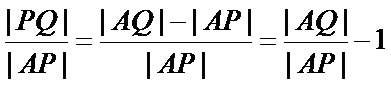
代入得到
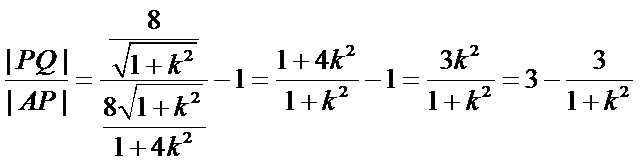
显然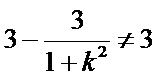
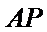
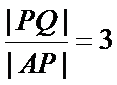
法二:(i)设点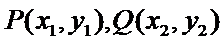
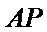
设直线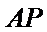
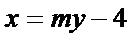
与椭圆方程联立得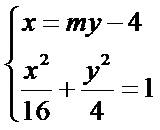
化简得到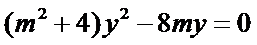
显然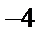
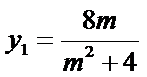
由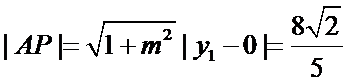
代入得到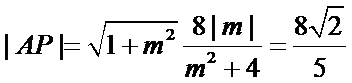
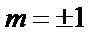
所以直线
(ii)因为圆心到直线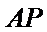
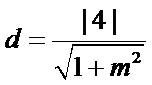
所以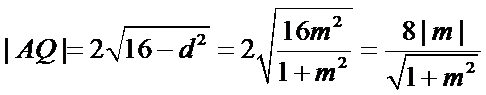
因为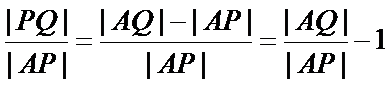
代入得到
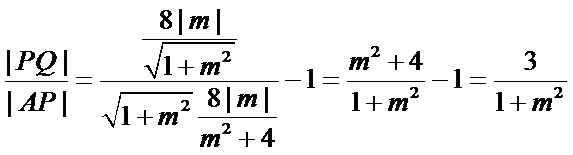
若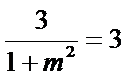
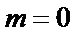
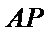
所以不存在直线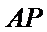
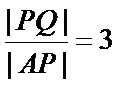
考查方向
本题考查了椭圆的综合求解能力,在近几年的各省高考题出现的频率较高.
解题思路
(Ⅰ)由椭圆的左顶点求出a,再有离心率求出c,进而求得b的值;
(Ⅱ)(i)联立方程,利用韦达定理求得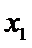
(ii)利用垂径定理求解.
易错点
计算量大,易出错.
知识点
17. 为了研究某种农作物在特定温度下(要求最高温度


(Ⅰ)根据本次试验目的和试验周期,写出农学家观察试验的起始日期.
(Ⅱ)设该地区今年10月上旬(10月1日至10月10日)的最高温度的方差和最低温度的方差分别为

(Ⅲ)从10月份31天中随机选择连续三天,求所选3天每天日平均最高温度值都在[27,30]之间的概率.
正确答案
(Ⅰ)7日或8日.
(Ⅱ)最高温度的方差大.
(Ⅲ)
解析
(Ⅰ)农学家观察试验的起始日期为7日或8日.
(Ⅱ)最高温度的方差大.
(Ⅲ)设“连续三天平均最高温度值都在[27,30]之间”为事件A,
则基本事件空间可以设为
由图表可以看出,事件A中包含10个基本事件,
所以
所选3天每天日平均最高温度值都在[27,30]之间的概率为
考查方向
本题考查了读图识图能力,在近几年的各省高考题出现的频率非常高.
解题思路
(Ⅰ)观察哪一段的温度在27度~30度之间;
(Ⅱ)观察数据的偏离程度;
(Ⅲ)求出基本事件空间.
易错点
基本事件空间计算错误.