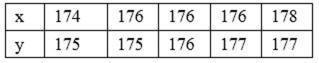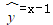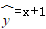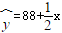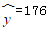- 真题试卷
- 模拟试卷
- 预测试卷
1．复数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．已知
A-5
B5
C-5
D5
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．下列命题中的真命题是（ ）
A若a>b>0，a>c，则a2> bc
B若a>b>c，则
C若a>b，n∈N*，则an>bn
D若a>b>0，则1na<1nb
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．执行程序框图，若输入x的值依次是：93，58，86，88，94，75，67，89，55，53，则输出m的值为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．设m，n是不同的直线，
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．如图是某同学一学期两次考试成绩的茎叶图，现从该同学两次考试成绩中各取一科成绩，则这两科成绩都在80分以上的概率为（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．如图，在矩形OABC中，点E，F分别在AB，BC上，且满足AB=3AE，BC=3CF，若
A
B
C
D1
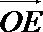
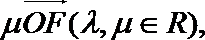
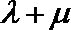
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．已知U＝{1,2,3,4,5,6,7,8}，A＝{1,3,5,7}，B＝{2,4,5}，则C
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．已知cos（
A
B
C-
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．在△ABC中，角A，B，C的对边分别是a，b，c，若B=2A，则
A(0，2)
B(1，2)
C（0，
D（
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11． 某变量x与y的数据关系如下：则y对x的线性回归方程为（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．已知定义域为R的函数y=f(x)在[0，7]上只有l和3两个零点，且y=f(2-x)与y=f (7+x)都是偶函数，则函数y=f(x)在[0，2013]上的零点个数为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．已知三棱锥P－ABC的底面是边长为3的等边三角形，PA⊥底面ABC，PA =2，则三棱锥P－ABC外接球的表面积为________。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．给出下列四个命题：
①函数f(x)=ex+ e－x有最小值2；
②函数f(x)=4sin(2x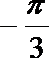
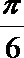
③一组数据的平均数一定不小于它的中位数；
④已知定义在R上的可导函数y=f(x)满足：对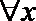
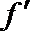
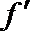
其中正确命题的序号是__________．（写出所有正确命题的序号）
正确答案
①②④
解析
解析已在路上飞奔，马上就到！
知识点
14．已知变量x，y满足约束条件
正确答案
5
解析
解析已在路上飞奔，马上就到！
知识点
13．若命题“
正确答案
（-2，2）
解析
解析已在路上飞奔，马上就到！
知识点
19．某学校为了了解高三学生的身体健康状况，在该校高三年级学生中随机抽取了100名学生进行调查，按日睡眠时间（单位：小时）分组得到如图1的频率分布表和如图2的频率分布直方图。
（Ⅰ）请补全频率分布直方图，并求频率分布表中的a，b；
（Ⅱ）现用分层抽样法从第一、二、五组中抽取6名学生进行体检，求第一、二、五组各应抽取多少名学生？
（III）在上述6名学生中随机抽取2名学生进行某专项体检，求这2名学生中恰有一名学生在第二组的概率。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17.阅读程序框图（图中n∈N*），回答下面的问题。
（Ⅰ）当n=3时，求S的值；
（Ⅱ）当S<100时，求n的最大值。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
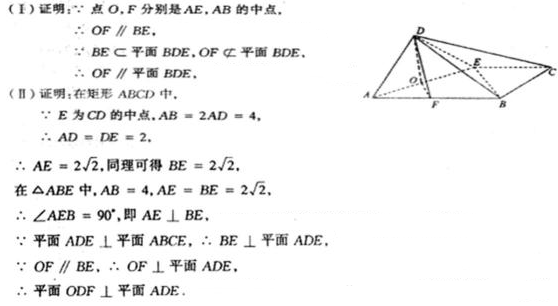
20. 已知矩形ABCD中，AB=2AD=4，E为CD的中点，沿AE将△ADE折起，使平面ADE上平面ABCE，点O、F分别是AE、AB的中点。
（Ⅰ）求证：OF∥平面BDE；
（Ⅱ）平面ODF⊥平面ADE．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18.已知a=（sin2x，2cos2x-1），b=(sin
（Ⅰ）求
（Ⅱ）当x∈
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21. 知函数f(x)=1nx－
（Ⅰ）当a=2时，求y=f(x)的单调区间和极值；
（Ⅱ）若y=f(x)存在单调递减区间，求a的取值范围。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
请在第22、23、24三题中任选一题做答。
22.选修4－1:几何证明选讲。
如图，⊙O1与⊙O2相交于点A，B，⊙O1的切线AC交⊙O2于另一点C，⊙O2的切线AD交⊙O1于另一点D，DB的延长线交⊙O2于点E。
（Ⅰ）求证：AB2=BC·BD;
（Ⅱ）若AB =1，AC =2，AD=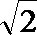
23.选修4-4：坐标系与参数方程
已知曲线C：y2= 4x，直线l过点P（-1，-2），倾斜角为30o，直线l与曲线C相交于A、B两点。
（Ⅰ）求直线l的参数方程；
（Ⅱ）求|PA |·|PB|的值。
24.选修4－5：不等式选讲
已知f(x) =|x+l|+|x-2|,g(x)=|x+l |－|x－a|+a(a∈R)。
（Ⅰ）解不等式f(x)≤5；
（Ⅱ）若不等式f(x)≥g(x)恒成立，求a的取值范围，
正确答案
22.
23.
24.
解析
解析已在路上飞奔，马上就到！