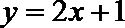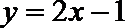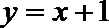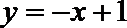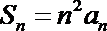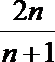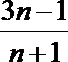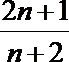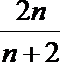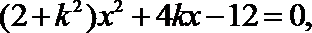- 真题试卷
- 模拟试卷
- 预测试卷
1.已知全集U=R,集合A={x|


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.i是虚数单位,若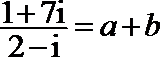
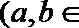
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.为了了解某校高三400名学生的数学学业水平测试成绩,制成样本频率分布直方图如图1,规定不低于60分为及格,不低于80分为优秀,则及格率与优秀人数分别是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.由代数式的乘法法则类比推导向量的数量积的运算法则:
①“mn=nm”类比得到“a

②“(m+n)t=mt+nt”类比得到“(a+b) 


③“




④“




⑤“|



以上式子中,类比得到的结论正确的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.曲线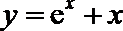
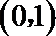
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在独立性检验中,统计量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知数列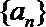
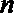
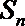
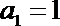
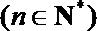
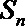
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数



正确答案
(-1,1)
解析
解析已在路上飞奔,马上就到!
知识点
15.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 某小卖部为了了解热茶销售量y(杯)与气温x(℃)之间的关系,随机统计了某4天卖出的热茶的杯数与当天气温,并制作了对照表,由表中数据算得线性回归方程

正确答案
70
解析
解析已在路上飞奔,马上就到!
知识点
16.在平面直角坐标系中,











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 设数列



(Ⅰ)求



(Ⅱ)用三段论证明数列
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知△





(1)若

(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知关于
(Ⅰ)设集合







(Ⅱ)设点





正确答案
则事件
(Ⅱ)依条件可知试验的全部结果所构成的区域为
其面积
事件
由


解析
解析已在路上飞奔,马上就到!
知识点
20.如图,已知两个正方形ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
(1)若平面
(2)用反证法证明:直线ME与BN是两条异面直线。
正确答案
(1)
取CD的中点G,连接MG,NG.
设正方形ABCD,DCEF的边长为2,
则
因为平面
所以
可得
因为
所以sin
即MN与平面DCEF所成角的正弦值为
(2)证明:假设直线ME与BN共面,
则
由已知,两正方形不共面,故
又AB∥CD,所以AB∥平面DCEF.
而EN为平面MBEN与平面DCEF的交线,所以AB∥EN.
又AB∥CD∥EF,所以EN∥EF,这与
所以直线ME与BN不共面,即它们是异面直线.
解析
解析已在路上飞奔,马上就到!
知识点
21. 设函数
(1)已知函数


(2)已知不等式


正确答案
(2)
解析
解析已在路上飞奔,马上就到!
知识点
22.已知椭圆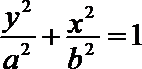
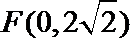
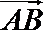
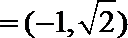
(1)求椭圆的方程;
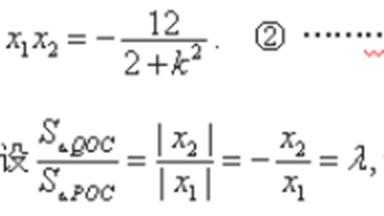
(2)若斜率为k的直线过点C(0,2),且与椭圆交于P,Q两点,求△POC与△QOC面积之比的取值范围。
正确答案
(1)由向量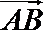
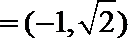
又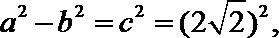
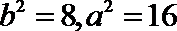
所以椭圆方程为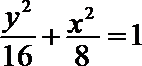
(2)设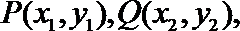

PQ方程为y=kx+2,代入椭圆方程并消去y,
得
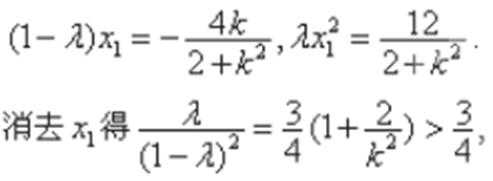
所以
解析
解析已在路上飞奔,马上就到!