文科数学昆明市2012年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1．集合，，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 5分

2．已知，为虚数单位，且，则的值为（）

B4+4

C-4

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：单选题

分值: 5分

5．设函数，曲线在点处的切线方程为，则曲线在点处切线的斜率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

9．在中，如果，，，则的面积为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

分值: 5分

3．下列判断错误的是（）

A“”是“a < b”的充分不必要条件

B命题“”的否定是“ ”

C在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高

D若为假命题, 则p, q均为假命题

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：单选题

分值: 5分

4．若函数对任意的都有，则等于（）

D-3

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

6．已知函数f（x）＝，若f （a）＋f （1）＝0，则实数a的值等于（）

A－3

D－1

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

8．若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

10．若直线2ax－by+2=0 （a >0, b>0）被圆x2+y2+2x－4y+1=0截得的弦长为4，则的最小值（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线的倾斜角与斜率

题型：单选题

分值: 5分

11．已知则关于x的方程有实根的概率是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：单选题

分值: 5分

12．关于的方程的两实根为，若，则的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

7．已知抛物线C的顶点为坐标原点，焦点在x轴上，直线y=x与抛物线C交于A、B两点，若点P （2,2）为AB的中点，则抛物线C的方程是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

填空题本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 5分

13．函数在区间[]的最小值为_________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

14．若以连续掷两次骰子分别得到的点数m,n作为P点的坐标,则点P在圆内的概率为_______

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

随机事件的关系

题型：填空题

分值: 5分

15．阅读下面的程序框图，则输出的=_________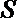

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

流程图的概念

题型：填空题

分值: 5分

16．正三棱锥P－ABC高为2，侧棱与底面所成角为45°，则点A到侧面PBC的距离________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

简答题（综合题）本大题共70分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

17．已知数列的前项和为，且是与2的等差中项；数列中，，点在直线上。

（Ⅰ）求数列的通项公式和；

（Ⅱ）设，求数列的前n项和。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：简答题

分值: 12分

18．如图，已知直三棱柱中，，，分别是棱，的中点．

（Ⅰ）求证：平面平面；

（Ⅱ）求证：平面。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：简答题

分值: 12分

19．甲乙两个学校高三年级分别有1100人，1000人，为了了解两个学校全体高三年级学生在该地区二模考试的数学成绩情况，采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩，并作出了频数分布统计表如下：

甲校：

乙校：

（Ⅰ）计算x，y的值。

（Ⅱ）若规定考试成绩在[120,150]内为优秀，请分别估计两个学校数学成绩的优秀率；

（Ⅲ）由以上统计数据填写下面2×2列联表，并判断是否有97．5%的把握认为两个学校的数学成绩有差异。

附：；

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法

题型：简答题

分值: 12分

20．已知函数

（I）当的单调区间和极值；

（II）若函数在[1，4]上是减函数，求实数的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

21．已知椭圆，过点的直线与原点的距离为。

（Ⅰ）求椭圆的方程；

（Ⅱ）直线与椭圆交于两点，以线段为直径的圆过点，求直线的方程。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

题型：简答题

分值: 10分

22．选考题：请在下列A、B、C三题中任选一题作答

A．【选修4-1:几何证明选讲】

如图，Δ是内接于⊙O，，直线切⊙O于点，弦，与相交于点．

（I）求证：Δ≌Δ；

（Ⅱ）若，求．

B．【选修4—4：坐标系与参数方程】

以直角坐标系的原点为极点，轴的正半轴为极轴，已知点的直角坐标为，点的极坐标为，若直线过点，且倾斜角为，圆以为圆心、为半径。

（I）写出直线的参数方程和圆的极坐标方程；

（Ⅱ）试判定直线和圆的位置关系。

C．【选修4—5：不等式选讲】

设函数＞1），且的最小值为，若，求的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷