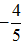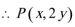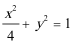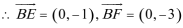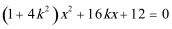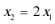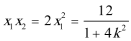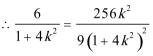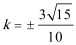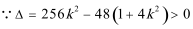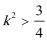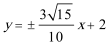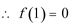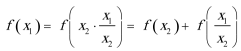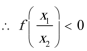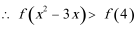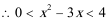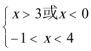- 真题试卷
- 模拟试卷
- 预测试卷
1.若集合

正确答案
0或4
解析
解析已在路上飞奔,马上就到!
知识点
6.已知某个几何体的三视图如图(主视图中的弧线是半圆),根据图中标出的尺寸(单位:

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.将3名学生安排到


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若对任意实数



正确答案
-243
解析
解析已在路上飞奔,马上就到!
知识点
11.定义





正确答案
(1,2009)
解析
解析已在路上飞奔,马上就到!
知识点
2.若复数



正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
3.若直线
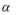
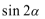
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.不等式组
正确答案
15
解析
解析已在路上飞奔,马上就到!
知识点
7.函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.数列





正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
14.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知两点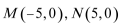
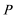
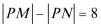
①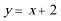
②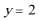
③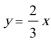
④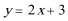
其中是“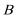
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数


正确答案
当




当


解析
解析已在路上飞奔,马上就到!
知识点
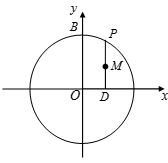
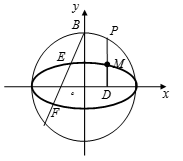
19.如图,圆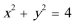
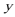
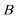
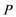
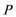
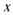
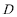
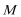
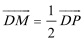
(1)求动点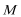
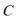
(2)过点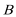
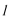
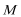
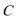
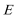
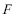
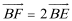
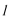
正确答案
(1)设轨迹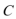

则由题意得: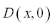
则
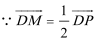
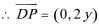

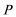
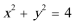
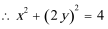
即动点
(2)当直线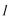
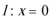
此时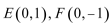
显然不满足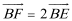
因此直线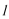
设直线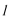
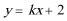
代入椭圆方程,
可得:
设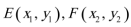
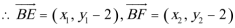
由题意知:
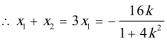
解此方程可得:
解得:
显然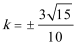

解析
解析已在路上飞奔,马上就到!
知识点
20.对于给定数列





(1)若






(2)若数列


(3)若数列








正确答案
(1)


又


对应的实常数为
(2)若数列


使得

且有

因此

故数列

(3)





若

由(2)知:

即存在实常数
使





此时





解析
解析已在路上飞奔,马上就到!
知识点
18.定义在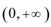
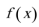

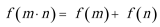
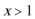
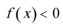
(1)求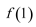
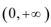
(2)当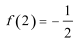
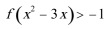
正确答案
(1)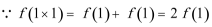
设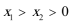
则
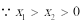
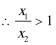

即函数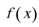
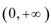
(2)
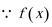
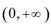
可得:
解此不等式组可得: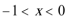
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)若函数


(2)当




(3)对于函数










正确答案
(1) 

设
则


(2)当

要使

即

只需






当


综上所述,当

当
(3)

且在
当

要使

只能满足


此时

即方程








此时

即
可得:


代入上式可得:
综上所述,
当


解析
解析已在路上飞奔,马上就到!