- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合A={x|1≤x≤4},B=Z为整数集,则A∩B=_________.
正确答案
{1,2,3,4}
解析
∵ 集合A={x|1≤x≤4},B=Z为整数集,
∴ A∩B={x|1≤x≤4}∩Z={1,2,3,4}.
故答案为:{1,2,3,4}.
知识点
2.函数y=cos2x﹣sin2x的最小正周期为_________.
正确答案
π
解析
解:y=
=
=
∴ 最小正周期为
故答案为π.
知识点
4.若函数f(x)=x2+|x+2a﹣1|+a的图象关于y轴对称,则实数a=_________.
正确答案
解析
∵ 函数f(x)=x2+|x+2a﹣1|+a的图象关于y轴对称,
∴ f(x)=f(﹣x),
即x2+|x+2a﹣1|+a=x2+|﹣x+2a﹣1|+a,
|x+2a﹣1|=|x﹣2a+1|,
2a﹣1=0
a=
知识点
7.偶函数f(x)在[0,+∞)上单调递增,且f(3)=0,若f(2x﹣1)<0,则实数x的取值范围是_________.
正确答案
(-1,2)
解析
∵ 偶函数f(x)在[0,+∞)上单调递增,且f(3)=0,
∴ f(2x﹣1)<0可化为
﹣3<2x﹣1<3,
解得﹣1<x<2,
故答案为:(﹣1,2).
知识点
9.若函数f(x)=cos2x+asinx在区间(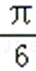
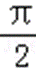
正确答案
解析
解:由f(x)=cos2x+asinx
=﹣2sin2x+asinx+1,
令t=sinx,
则原函数化为y=﹣2t2+at+1.
∵ x∈(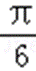
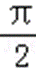
则y=﹣2t2+at+1在t∈(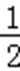
∵ y=﹣2t2+at+1的图象开口向下,且对称轴方程为t=
∴ 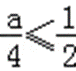
∴ a的取值范围是(﹣∞,2].
故答案为:(﹣∞,2].
知识点
3.函数y=x2﹣1(x<﹣1)的反函数是_________.
正确答案
y=﹣
解析
解:由y=x2﹣1(x<﹣1),
解得
把x与y互换可得y=﹣
∴ 函数y=x2﹣1(x<﹣1)的反函数是y=﹣
故答案为:y=﹣
知识点
5.已知logab=﹣1,则a+2b的最小值是_________.
正确答案
解析
解:由于logab=﹣1,
则b=
则a+2b=a+


当且仅当a=

故答案为:2
知识点
6.幂函数f(x)=(m2﹣m+1)xm的图象与y轴没有交点,则m=_________.
正确答案
0
解析
解:根据幂函数的定义,得;
m2﹣m+1=1,
解得m=0或m=1;
当m=0时,f(x)=x0,图象与y轴没有交点,满足题意;
当m=1时,f(x)=x,图象与y轴有交点,不满足题意;
综上,m=0.
故答案为:0.
知识点
8.不等式
正确答案
(-2,2)
解析
解:由题意,考察y=
∵ 
∴ x2+ax>2x+a﹣2恒成立
∴ x2+(a﹣2)x﹣a+2>0恒成立
∴ △=(a﹣2)2﹣4(﹣a+2)<0
即(a﹣2)(a﹣2+4)<0
即(a﹣2)(a+2)<0
故有﹣2<a<2,即a的取值范围是(﹣2,2)
故答案为(﹣2,2)
知识点
10.已知f(x)是定义在[﹣2,2]上的函数,对于任意实数x1,x2∈[﹣2,2],且x1≠x2时,恒有,
正确答案
4
解析
∵ f(x)是定义在[﹣2,2]上的函数,
对于任意实数x1,x2∈[﹣2,2],且x1≠x2时,
恒有,
∴ f(x)在[﹣2,2]上是单调递增数,
∵ f(x)的最大值为1,
∴ f(2)=1
∵ f(log2x)=1,
∴ log2x=2,x=4
知识点
11.设函数f(x)=x2+loga(bx+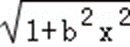
正确答案
3.3
解析
∵ f(x)=x2+loga(bx+
∴ f(2)=4+loga(2b+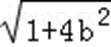
解得loga(2b+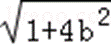
∴ f(﹣2)=4+loga(﹣2b+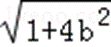
=4﹣loga(2b+
=4﹣0.7
=3.3.
知识点
12.已知AB=2,∠B=60°,AC=b,若b∈M时△ABC能唯一确定,则集合M=_________.
正确答案
解析
∵ △ABC中,∠ABC=60°,AC=b,AB=2,
∴ 由正弦定理





∵ 0 °<C<120°,∴0<sinC≤1,
且b≥2,
则b的取值范围为M=[2,+∞)∪ {
知识点
14.若定义在R上的函数f(x)是奇函数,f(x﹣2)是偶函数,且当0<x≤2时,f(x)=
正确答案
24
解析
∵ 定义在R上的函数f(x)是奇函数,
∴ f(﹣x)=﹣f(x),
∵ f(x﹣2)是偶函数,
∴ f(x﹣2)=f(﹣x﹣2),
f(2﹣x)=f(2+x),
即f(x)=f(4﹣x),
f(x+4)=﹣f(x),
∴ f(x+8)=f(x),
可得周期为8,x=2为对称轴,
∵ f(x)=f(3),
∴ x1=1,x2=3,x3=9,x4=11,x5=17,x6=19,
∵ 在区间(0,16)上的所有实数根之和,
∴ x1+x2+x3+x4=1+3+9+11=24,
知识点
13.已知P1(x1,x2),P2(x2,y2)是以原点O为圆心的单位圆上的两点,∠P1OP2=θ(θ为钝角).若sin(

正确答案
解析
由题意可得


∴ 


∴ 
∴ cosθ=﹣
∴ 





知识点
19.设函数sgn(x)=
正确答案
解:①当lnx>0,即x>1时,
f(x)=sgn(lnx)﹣ln2x=0可化为:1﹣ln2x=0,
解得,x=e;
②当lnx=0,即x=1时,
f(x)=sgn(lnx)﹣ln2x=0可化为0﹣ln21=0,显然成立;
③当lnx<0,即0<x<1时,
f(x)=sgn(lnx)﹣ln2x=0可化为:
﹣1﹣ln2x=0,
无解;
综上所述,
x=e或x=1.
解析
解析已在路上飞奔,马上就到!
知识点
20.解下列不等式:
(1)|x﹣1|+|x﹣2|<2;
(2)0<x﹣
正确答案
解:(1)∵ 数轴上0.5与2.5到1与2的距离均为2,
∴ 由|x﹣1|+|x﹣2|<2,得

∴ 原不等式的解集为{x|

(2)∵ 0<x﹣
∴
解①得:﹣1<x<0或x>1;
解②得:x<

综合①②得,﹣1<x<

解析
解析已在路上飞奔,马上就到!
知识点
21.定义:若对任意x1、x2∈(a,b)恒有f(



(1)试判断y=x2是否为R上的凹函数,并说明理由;
(2)若x、y、z∈R,且x+y+2z=8,试求x2+y2+2z2的最小值并指出取得最小值时x、y、z的值.
正确答案
解:(1)f(





∴ 对任意x1、x2∈(a,b)恒有f(

∴ y=x2是R上的凹函数;
(2)∵(x2+y2+2z2)(12+12+
∴ x2+y2+2z2≥16,当且仅当x=y=
∵ x+y+2z=8,∴ x=y=4(

∴ x2+y2+2z2的最小值为16,
此时x=y=4(

解析
解析已在路上飞奔,马上就到!
知识点
23.在△ABC中,设角A、B、C的对边分别为a、b、c,且a≤b≤c,
(1)若b2=ac,求角B的取值范围;
(2)求证:以
(3)当0≤x≤1时,以ax、bx、cx为长的线段是否一定能构成三角形?写出你的结论,并说明理由.
正确答案
解:(1)∵在△ABC中,b2=ac,
∴由余弦定理得:cosB=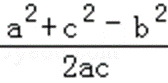
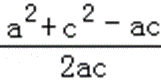

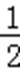
则B的范围为(0,60°].
(2)由a≤b≤c,得到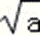
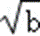
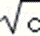
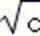
由余弦定理得:cosα=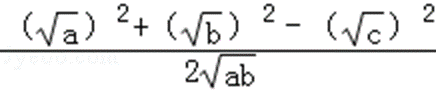
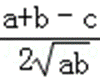
∵a,b,c为△ABC的三边,∴a+b>c,即a+b﹣c>0,2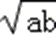
∴cosα>0,即α为锐角,
则以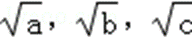
(3)当0≤x≤1时,由a≤b≤c,可得ax ≤bx ≤cx,
∵ax+bx﹣cx=cx•[




故较小的两边之和大于较大的一边,故以ax、bx、cx为长的线段一定能构成三角形.
解析
解析已在路上飞奔,马上就到!
知识点
22.已知二次函数f(x)=ax2+bx+1和函数g(x)=
(1)若g(x)是奇函数,试求f(x)在R上的值域;
(2)若方程g(x)=x有两个不相等的实根,当b>0时,判断f(x)在(﹣1,1)上的单调性;
(3)若方程g(x)=x的两实根为x1,x2f(x)=0的两根为x3,x4,求使x3<x1<x2<x4成立的a的取值范围.
正确答案
解:(1)因为g(x)为奇函数,
所以g(﹣x)=﹣g(x),
又函数g(x)=
则

化简可得b=0,
所以f(x)=ax2+1,定义域为R,
所以函数f(x)的值域为[1,+∞);
(2)由方程g(x)=x整理可得a2x2+bx+1=0,
因为方程g(x)=x有两个不相等的实根,
所以△=b2﹣4a2>0,即|


又因为函数f(x)=ax2+bx+1的对称轴为x=﹣
所以当﹣
当﹣
(3)由

设α为x1与x2中的一个数,
则有
因为x3+x4=﹣

所以有
当a>0时有
所以结合两式可得(a﹣a2)α2<0,
解得:a>1或a<0(舍去).
当a<0时有
所以所以结合两式可得(a﹣a2)α2>0,
解得:0<a<1(舍去).
综上可得a的取值范围为(1,+∞).
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数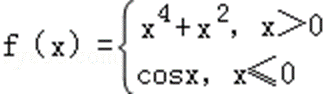
正确答案
解析
选项A,
∵ 函数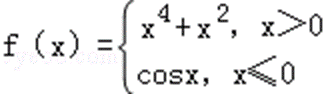
∴ f(1)=14+12=2,
f(﹣1)=cos(﹣1)=cos1≠2.
∴ f(﹣x)=f(x).
∴ f(x)不是偶函数;
选项B,
当x=﹣2π时,f(﹣2π)=cos(﹣2π)=1,
当x=﹣π时,f(﹣π)=cos(﹣π)=﹣1,
∵ ﹣2π<﹣π,f(﹣2π>f(﹣π),
∴ f(x)在(﹣∞,+∞)上不是增函数;
选项C,
∵ f(x)在(0,+∞)是增函数;
∴ f(x)不是周期函数;
选项D,
当x>0时,y=x4+x2>0,
当x≤0时,y=cosx∈[﹣1,1],
∴ f(x)的值域为[﹣1,+∞).
故选D.
知识点
16.已知a,b都是实数,那么“a2>b2”是“a>b”的( )
正确答案
解析
∵ “a2>b2”既不能推出“a>b”;
反之,由“a>b”也不能推出“a2>b2”.
∴ “a2>b2”是“a>b”的既不充分也不必要条件.
故选D.
知识点
17.若M={(x,y)||tanπy|+sin2πx=0},N={(x,y)|x2+y2≤2},则M∩N的元素个数是( )
正确答案
解析
∵ M={(x,y)||tanπy|+sin2πx=0},
∴ 集合M是整数点的集合,
∵ N={(x,y)|x2+y2≤2}表示圆心为(0,0),半径为
∴ M∩N={(0,0),(0,1),(0,﹣1),(1,0),
(﹣1,0),(1,1),(1,﹣1),(﹣1,1),(﹣1,﹣1)},
∴ M∩N的元素个数是9个.
故选D.
知识点
18.已知f(x)=3x2﹣x+4,f[g(x)]=3x4+18x3+50x2+69x+48,那么整系数多项式函数g(x)的各项系数和为( )
正确答案
解析
由题意得g(x)的表达式是二次式,
设g(x)=ax2+bx+c,
∴ f[g(x)]=3(ax2+bx+c)2﹣(ax2+bx+c)+4
=3a2x4+6abx3+(3b2+6ac﹣a2)x2+(6bc﹣b)x+3c2﹣c+4
=3x4+18x3+50x2+69x+48,
∴ 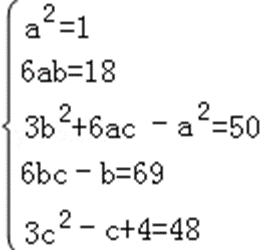
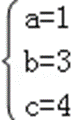
∴ a+b+c=8,
故选:A.