- 真题试卷
- 模拟试卷
- 预测试卷
2.将函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.甲、乙两人下棋,两人下成和棋的概率是


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.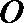
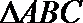
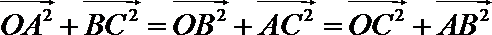
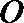
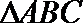
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.曲线

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
11.若以连续掷两次骰子分别得到的点数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若集合


正确答案
充分不必要
解析
解析已在路上飞奔,马上就到!
知识点
13.已知



正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
12.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.定义
正确答案
②
解析
解析已在路上飞奔,马上就到!
知识点
15.给出下列命题:
①若
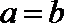
②若A,B,C,D是不共线的四点,则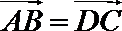
③若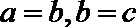
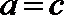
④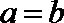

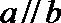
⑤若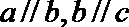
其中正确的序号是__________
正确答案
②④
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知函数

(1)当

(2)若函数


(3)若对于任意的



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 设






(1)求
(2)试写出一个解集为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知A,B,C是△ABC的三内角,向量
(1)求角A;
(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数



(1)求函数
(2)若数列



(3)在(2)的条件下,证明:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 请你把“若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 某上市股票在30天内每股的交易价格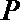

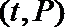
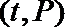
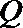
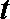
(1)根据提供的图象,写出该种股票每股交易价格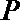
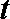
(2)根据表中数据确定日交易量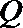

(3)在(2)的结论下,用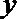
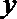
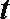
正确答案
解析
解析已在路上飞奔,马上就到!