- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设f:A→B是集合A到B的映射,下列命题中是真命题的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若 



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知数列{an}满足a1 =0,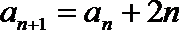
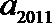
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数f(x)=Asin(ωx+ψ)(A>O,ω>0)的部分图象如图所示,则f(1)+f(2)+…+f(2011) 的值等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知等比数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.有下列四个命题:
①“若xy=1,则x、y互为倒数”的逆命题;
②“相似三角形的周长相等”的否命题;
③“若b≤-1,则方程x2-2bx+b2+b=0有实根”的逆命题;
④
其中真命题的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.如图,半圆的直径AB=6,O为圆心,C为半圆上不同于A、B的任意一点,若P为半径OC上的动点,则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设集合A={5,log2(a+3)},集合B={a,b}.若A∩B={2},则A∪B=( )
正确答案
{1,2,5}
解析
解析已在路上飞奔,马上就到!
知识点
14.如图所示,已知梯形ABCD中,AB∥CD,且AB=3CD,M,N分别是AB,CD的中点,设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.为测量某塔AB的高度,在一幢与塔AB相距20 m的楼顶处测得塔顶A的仰角为30°,测得塔基B的俯角为45°,那么塔AB的高度是( ) m.
正确答案
20(1+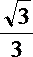
解析
解析已在路上飞奔,马上就到!
知识点
16.将全体正整数排成一个三角形数阵:
按照以上排列的规律,第

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知向量

(1)求函数

(2)若方程





正确答案
(1)
最大值为2,相应的
最小值为-2,相应的
(2)


在同一坐标系中作出


当

当

解析
解析已在路上飞奔,马上就到!
知识点
18.设{an}为等差数列,Sn为数列{an}的前n项和,已知
(1)求{an}的通项公式;
(2)若


正确答案
(1)设等差数列{an}的公差为d,则Sn=na1+
∵S7=7,S15=75,∴
即

所以
(2)∴


∵




∴Tn=

解析
解析已在路上飞奔,马上就到!
知识点
19.设p:实数x满足x2-4ax+3a2<0,其中a<0;q:实数x满足x2-x-6≤0,或x2+2x-8>0,且
正确答案
设A={x|p}={x|x2-4ax+3a2<0,a<0}={x|3a<x<a,a<0},
B={x|q}={x|x2-x-6≤0或x2+2x-8>0}={x|x2-x-6≤0}∪{x|x2+2x-8>0}
={x|-2≤x≤3}∪{x|x<-4或x>2}=
∵

则


∴
则
(法二)即:
可得-
解析
解析已在路上飞奔,马上就到!
知识点
20.已知向量






(Ⅰ) 

(Ⅱ)若f(x)= 


正确答案
(Ⅰ) 

x∈[0, 
∴ 
(Ⅱ)f(x)=cos2x-4λcosx=2cos2x-1-4λcosx,设t=cosx,
则
即y=f(x)=2t2-4λt-1=2(t-λ)2-1-2λ2.
①λ<0时,当且仅当t=0时,y取最小值-1,这与已知矛盾
②当0≤λ≤1时,当且仅当t=λ时,y取得最小值-1-2λ2,
由已知得
③当λ>1时,当且仅当t=1时,y取得最小值1-4λ.
由已知得

综上λ=
解析
解析已在路上飞奔,马上就到!
知识点
21.函数
(1)若


(2)若
正确答案
(1)①若
1)当a=1时,
2)当a=-1时,
②若



综合①、②得a的取值范围
(2)命题等价于不等式
显然




解析
解析已在路上飞奔,马上就到!
知识点
22.给出下面的数表序列:
其中表n(n=1,2,3 

(I)写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表n(n≥3)(不要求证明);
(II)每个数列中最后一行都只有一个数,它们构成数列1,4,12



正确答案
(Ⅰ)表4为
它的第1,2,3,4行中的数的平均数分别是4,8,16,32,它们构成首项为4,公比为2的等比数列。
将这一结论推广到表

简证如下(对考生不作要求)
首先,表

其平均数为
其次,若表


则它的第

由等差数列的性质知,表


由此可知,表
且各行中的数的平均数按从上到下的顺序构成首项为
(Ⅱ)表

由(Ⅰ)知,它的各行中的数的平均数按从上到下的顺序构成首项为



因此
故
解析
解析已在路上飞奔,马上就到!


























































