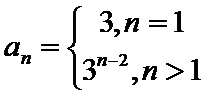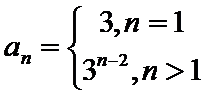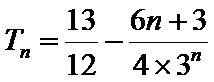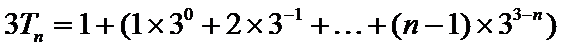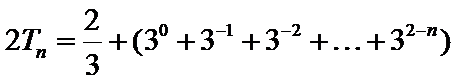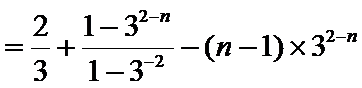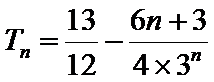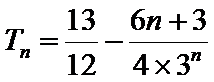• 职业资格类
  • 建筑类
  • 学历类
  • 财会类
  • 医药类
  • 全部考试
  • 教师招募
职业资格类
建筑类
学历类
财会类
计算机类
公务员
医药类
2015年高考真题 理科数学 (山东卷)
精品
|
立即下载

理科数学 热门试卷

X 查看更多试卷
试卷目录
1、单选题
1
2
3
4
5
6
7
8
9
10
2、填空题
11
12
13
14
15
3、简答题
16
17
18
19
20
21
  • 真题试卷
  • 模拟试卷
  • 预测试卷
查看更多 >
单选题 本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。
1
题型： 单选题
|
分值: 5分

1．已知集合A={x|x2﹣4x+3＜0}，B={x|2＜x＜4}，则A∩B=（　　）

A（1，3）

B（1，4）

C(2,3)

D(2,4)

正确答案

C

解析

集合A={x|x2﹣4x+3＜0}={x|1＜x＜3}，B={x|2＜x＜4}，则A∩B={x|2＜x＜3}=

（2，3）．故选：C．

考查方向

本题考查集合的交集的求法，考查计算能力．

解题思路

求出集合A，然后求出两个集合的交集．

易错点

交集及其运算，注意数形结合思想的应用．菁优网版权所有

知识点

并集及其运算
1
题型： 单选题
|
分值: 5分

3．要得到函数的图象，只需将函数y=sin4x的图象（　　）

A向左平移个单位

B向右平移个单位

C向左平移个单位

D向右平移个单位

正确答案

B

解析

因为函数=sin[4（x﹣）]，要得到函数y=sin（4x﹣）的图象，只需将函数y=sin4x的图象向右平移单位．故选：B．

考查方向

本题考查三角函数的图象的平移，值域平移变换中x的系数是易错点．

解题思路

直接利用三角函数的平移原则推出结果即可．

易错点

函数y=Asin（ωx+φ）的图象变换，平移量的确定．菁优网版权所有

知识点

幂函数图象及其与指数的关系
1
题型： 单选题
|
分值: 5分

6．已知x，y满足约束条件，若z=ax+y的最大值为4，则a=（　　）

A3

B2

C-2

D-3

正确答案

B

解析

作出不等式组对应的平面区域如图：（阴影部分）．则A（2，0），B（1，1），

若z=ax+y过A时取得最大值为4，则2a=4，解得a=2，

此时，目标函数为z=2x+y，即y=﹣2x+z，

平移直线y=﹣2x+z，当直线经过A（2，0）时，截距最大，此时z最大为4，满足条件，

若z=ax+y过B时取得最大值为4，则a+1=4，解得a=3，

此时，目标函数为z=3x+y，即y=﹣3x+z，

平移直线y=﹣3x+z，当直线经过A（2，0）时，截距最大，此时z最大为﹣6，不满足条件，

故a=2，故选：B.

考查方向

本题主要考查线性规划的应用，结合目标函数的几何意义，利用数形结合的数学思想是解决此类问题的基本方法，确定目标函数的斜率关系是解决本题的关键．

解题思路

作出不等式组对应的平面区域，利用目标函数的几何意义，利用数形结合确定z的最大值．

易错点

线性规划中平面区域以及目标函数的几何意义．菁优网版权所有

知识点

简单复合函数的导数
1
题型： 单选题
|
分值: 5分

2．若复数z满足，其中i为虚数单位，则z=（　　）

A1﹣i

B1+i

C﹣1﹣i

D﹣1+i

正确答案

A

解析

，则z=i（1﹣i）=1+i，可得z=1﹣i．故选：A．

考查方向

本题考查复数的基本运算，基本知识的考查．

解题思路

直接利用复数的乘除运算法则化简求解即可．

易错点

复数代数形式的乘除运算，共轭的理解．菁优网版权所有

知识点

复数代数形式的乘除运算
1
题型： 单选题
|
分值: 5分

4．已知菱形的边长为 ，  ,则（    ）

A

B

C

D

正确答案

D

解析

∵菱形ABCD的边长为a，∠ABC=60°，∴=a2，=a×a×cos60°=，则（）•=+=，故选：D.

菁优网版权所有【解题思路】由已知可求，，根据（）•=+代入可求.

考查方向

本题主要考查了平面向量数量积的定义的简单运算，属于基础试题

易错点

平面向量数量积的运算，线性转换．

知识点

空间向量的数乘运算
1
题型： 单选题
|
分值: 5分

5．不等式|x﹣1|﹣|x﹣5|＜2的解集是（　　）

A

（﹣∞，4）

B（﹣∞，1）

C（1，4）

D（1，5）

正确答案

A

解析

①当x＜1，不等式即为﹣x+1+x﹣5＜2，即﹣4＜2成立，故x＜1；

②当1≤x≤5，不等式即为x﹣1+x﹣5＜2，得x＜4，故1≤x＜4；

③当x＞5，x﹣1﹣x+5＜2，即4＜2不成立，故x∈∅．

综上知解集为（﹣∞，4）．故选A．

考查方向

本题考查绝对值不等式的解法，主要考查运用零点分区间的方法，考查运算能力，属于中档题．

解题思路

运用零点分区间，求出零点为1，5，讨论①当x＜1，②当1≤x≤5，③当x＞5，分别去掉绝对值，解不等式，最后求并集即可．

易错点

绝对值不等式的解法，去绝对值的方法．菁优网版权所有

知识点

指数函数的图像变换
1
题型： 单选题
|
分值: 5分

7．在梯形ABCD中，，AD∥BC，BC=2AD=2AB=2，将梯形ABCD绕AD所在

的直线旋转一周而形成的曲面所围成的几何体的体积为（　　）

A

B

C

D [来源:学科网ZXXK]

正确答案

C

解析

由题意可知几何体的直观图如图：旋转体是底面半径为1，高为2的圆锥，挖去一个相同底面高为1的倒圆锥，几何体的体积为：．

故选：C．

考查方向

本题考查几何体的体积的求法，考查空间想象能力以及计算能力．画出几何体的直观图是解题的关键．

解题思路

画出几何体的直观图，利用已知条件，求解几何体的体积即可．

易错点

无图几何体的结构特征、组合体的体积。

知识点

简单复合函数的导数
1
题型： 单选题
|
分值: 5分

8．已知某批零件的长度误差（单位：毫米）服从正态分布N（0，32），从中随机抽取一件，其长度误差落在区间（3，6）内的概率为（　　）

（附：若随机变量ξ服从正态分布N（μ，σ2），则P（μ﹣σ＜ξ＜μ+σ）=68.26%，P（μ﹣2σ＜ξ＜μ+2σ）=95.44%）

A4.56%

B13.59%

C27.18%

D31.74%

正确答案

B

解析

由题意P（﹣3＜ξ＜3）=68.26%，P（﹣6＜ξ＜6）=95.44%，

所以P（3＜ξ＜6）=（95.44%﹣68.26%）=13.59%．故选：B．

考查方向

本题考查正态分布曲线的特点及曲线所表示的意义，考查正态分布中两个量μ和σ的应用，考查曲线的对称性，属于基础题．

解题思路

由题意P（﹣3＜ξ＜3）=68.26%，P（﹣6＜ξ＜6）=95.44%，可得P（3＜ξ＜6）=（95.44%﹣68.26%），即可得出结论．

易错点

正态分布曲线的特点及曲线所表示的意义．菁优网版权所有

知识点

一元高次不等式的解法
1
题型： 单选题
|
分值: 5分

9．一条光线从点（﹣2，﹣3）射出，经y轴反射后与圆（x+3）2+（y﹣2）2=1相切，则反射光线所在直线的斜率为（　　）

A或

B 或

C或

D或

正确答案

D

解析

点A（﹣2，﹣3）关于y轴的对称点为A′（2，﹣3），

故可设反射光线所在直线的方程为：y+3=k（x﹣2），化为kx﹣y﹣2k﹣3=0．

∵反射光线与圆（x+3）2+（y﹣2）2=1相切，

∴圆心（﹣3，2）到直线的距离d==1，

化为24k2+50k+24=0，∴k=或﹣．故选：D．

考查方向

圆的切线方程；直线的斜率．菁优网版权所有

解题思路

点A（﹣2，﹣3）关于y轴的对称点为A′（2，﹣3），可设反射光线所在直线的方程为：y+3=k（x﹣2），利用直线与圆相切的性质即可得出．

知识点

二次函数的应用
1
题型： 单选题
|
分值: 5分

10．设函数则满足的取值范围是（   ）

A

B

C

D

正确答案

C

解析

令fA.=t，则f（t）=2t，

当t＜1时，3t﹣1=2t，

由g（t）=3t﹣1﹣2t的导数为g′（t）=3﹣2tln2，

在t＜1时，g′（t）＞0，g（t）在（﹣∞，1）递增，

即有g（t）＜g（1）=0，则方程3t﹣1=2t无解；

当t≥1时，2t=2t成立，

由fA.≥1，即3a﹣1≥1，解得a≥，且a＜1；

或a≥1，2a≥1解得a≥0，即为a≥1．

综上可得a的范围是a≥．故选C．

考查方向

本题考查分段函数的运用，主要考查函数的单调性的运用，运用分类讨论的思想方法是解题的关键．

解题思路

令fA.=t，则f（t）=2t，讨论t＜1，运用导数判断单调性，进而得到方程无解，讨论t≥1时，以及a＜1，a≥1，由分段函数的解析式，解不等式即可得到所求范围．

易错点

分段函数的应用．菁优网版权所有

知识点

不等式恒成立问题
填空题 本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。
1
题型：填空题
|
分值: 5分

11．观察下列各式：

……

照此规律，当nN时，

              .

正确答案

4n﹣1

解析

因为；

…

照此规律，可以看出等式左侧最后一项，组合数的上标与等式右侧的幂指数相同，

可得：当n∈N*时，4n﹣1；

故答案为：4n﹣1．

考查方向

本题考查归纳推理的应用，找出规律是解题的关键．

解题思路

仔细观察已知条件，找出规律，即可得到结果．

易错点

归纳推理；组合及组合数公式．菁优网版权所有

知识点

等比数列的性质及应用
1
题型：填空题
|
分值: 5分

12．若“x[0,]，tanxm”是真命题，则实数m的最小值为　　．

正确答案

1

解析

“x[0,]，tanxm”是真命题，可得tanx≤1，所以，m≥1，

实数m的最小值为：1．故答案为：1．

考查方向

本题考查函数的最值的应用，命题的真假的应用，考查计算能力．

解题思路

求出正切函数的最大值，即可得到m的范围．

易错点

命题的真假判断与应用．菁优网版权所有

知识点

全（特）称命题的否定
1
题型：填空题
|
分值: 5分

14．已知函数f（x）=ax+b（a＞0，a≠1）的定义域和值域都是[﹣1，0]，则a+b=　　．

正确答案

-

解析

当a＞1时，函数f（x）=ax+b在定义域上是增函数，

所以解得b=﹣1，=0不符合题意舍去；

当0＜a＜1时，函数f（x）=ax+b在定义域上是减函数，

所以解得b=﹣2，a=

综上a+b=-，故答案为﹣.

考查方向

本题考查指数函数的单调性的应用，以及分类讨论思想，属于基础题

解题思路

对a进行分类讨论，分析题意和指数函数的单调性列出方程组求解。

易错点

函数的值域．菁优网版权所有

知识点

函数单调性的性质
1
题型：填空题
|
分值: 5分

15．平面直角坐标系xOy中，双曲线C1：（a>0,b>0）的渐近线与抛物线C2：X2=2py(p>0)交于O，若△OAB的垂心为C2的焦点，则C1的离心率为  ＿＿＿

正确答案

解析

双曲线C1：（a＞0，b＞0）的渐近线方程为y=±x，

与抛物线C2：x2=2py联立，可得x=0或x=±，

取A（，），则，

∵△OAB的垂心为C2的焦点，

∴（﹣）=﹣1，

∴5a2=4b2，∴5a2=4（c2﹣a2）

∴e==．故答案为：．

考查方向

本题考查双曲线的性质，考查学生的计算能力，确定A的坐标是关键．

解题思路

求出A的坐标，可得，利用△OAB的垂心为C2的焦点，可得（﹣）=﹣1，由此可求C1的离心率．

易错点

双曲线的简单性质．菁优网版权所有

知识点

数量积表示两个向量的夹角
1
题型：填空题
|
分值: 5分

13．执行如图程序框图，输出的T的值为　　．

正确答案

解析

模拟执行程序框图，可得n=1，T=1

满足条件n＜3，T=1+xdx，n=2

满足条件n＜3，T=1+xdx+x2dx=1+，n=3

不满足条件n＜3，退出循环，输出T的值为．

故答案为：.

考查方向

本题主要考查了循环结构的程序框图，考查了定积分的应用，属于基本知识的考查．

解题思路

模拟执行程序框图，依次写出每次循环得到的n，T的值，当n=3时不满足条件n＜3，退出循环，输出T的值为．

易错点

程序框图条件的执行与终止．菁优网版权所有

知识点

选择结构
简答题（综合题） 本大题共75分。简答应写出文字说明、证明过程或演算步骤。
1
题型：简答题
|
分值: 13分

若n是一个三位正整数，且n的个位数字大于十位数字，十位数字大于百位数字，则称n为“三位递增数”（如137，359，567等）．在某次数学趣味活动中，每位参加者需从所有的“三位递增数”中随机抽取1个数，且只能抽取一次，得分规则如下：若抽取的“三位递增数”的三个数字之积不能被5整除，参加者得0分，若能被5整除，但不能被10整除，得﹣1分，若能被10整除，得1分．

22.写出所有个位数字是5的“三位递增数”；

23.若甲参加活动，求甲得分X的分布列和数学期望EX．

第(1)小题正确答案及相关解析

正确答案

125，135，145，235，245，345；

解析

（I）个位数是5的“三位递增数”有

考查方向

考查排列组合的数字问题。

解题思路

（Ⅰ）根据“三位递增数”的定义，即可写出所有个位数字是5的“三位递增数”；

易错点

列举数字时注意不重复不遗漏

第(2)小题正确答案及相关解析

正确答案

【答案】的分布列为

则

解析

【解析】（II）由题意知，全部“三位递增数”的个数为，

随机变量是取值为：0，-1,1，因此

，

，

所以的分布列为

则

菁优网版权所有【分值】8分

考查方向

本题主要考查离散型随机变量的分布列和期望的计算，求出对应的概率是解决本题的关键．

解题思路

（Ⅱ）随机变量X的取值为：0，﹣1，1分别求出对应的概率，即可求出分布列和期望．

易错点

离散型随机变量的分布列及其期望的计算

1
题型：简答题
|
分值: 12分

设数列{an}的前n项和为Sn，已知2Sn=3n+3．

20.求{an}的通项公式；

21.若数列{bn}，满足anbn=log3an，求{bn}的前n项和Tn．

第(1)小题正确答案及相关解析

正确答案

（1）

解析

（I）因为，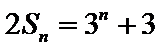

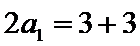
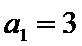
所以，故 ，

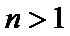
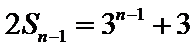
当时，，

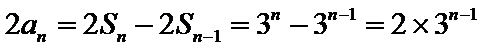
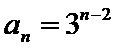
此时 ，即，

所以

考查方向

考查等差数列的通项公式的求法

解题思路

运用从一般到特殊的处理方法，准确确定等差数列的通项公式。

（Ⅰ）利用2Sn=3n+3，可求得a1=3；当n＞1时，2Sn﹣1=3n﹣1+3，两式相减2an=2Sn﹣2Sn﹣1，可求得an=3n﹣1，从而可得{an}的通项公式。

第(2)小题正确答案及相关解析

正确答案

（2）

解析

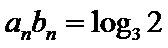
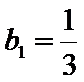
（II）因为，所以 ，

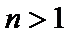
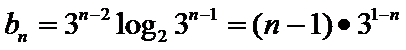
当时，，

所以；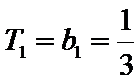

，

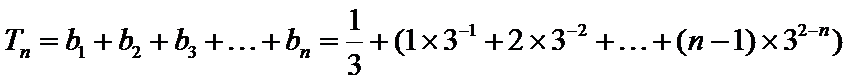
所以

两式相减，得

，

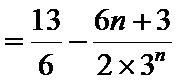
所以

经检验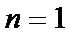，也适合，

综上可得

考查方向

本题考查数列的求和，着重考查数列递推关系的应用，突出考“查错位相减法”求和，考查分析、运算能力，属于中档题．

解题思路

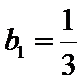
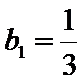
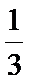
（Ⅱ）依题意，anbn=log3an，可得，当n＞1时，bn=31﹣n•log33n﹣1=（n﹣1）×31﹣n，于是可求得T1=；当n＞1时，Tn=b1+b2+…+bn=+（1×3﹣1+2×3﹣2+…+（n﹣1）×31﹣n），利用错位相减法可求得{bn}的前n项和Tn．

易错点

数列的错位相减求和时错项的处理，等差数列与等比数列的性质．

1
题型：简答题
|
分值: 12分

平面直角坐标系中，已知椭圆C: 的离心率为且点,) 在椭圆C上.

24.求椭圆C的方程；

25.设椭圆E:,P为椭圆C上任意一点，过点P的直线交椭圆E于A,B两点，射线PO交椭圆E于点Q.

(i)求的值；

(ii)求面积的最大值.

第(1)小题正确答案及相关解析

正确答案

.

解析

（I）由题意知，则，

又，可得 ,

所以椭圆的方程为.

考查方向

本题考查椭圆的方程和性质。

解题思路

（Ⅰ）运用椭圆的离心率公式和a，b，c的关系，计算即可得到b，进而得到椭圆C的方程；

易错点

椭圆方程中系数的求解

第(2)小题正确答案及相关解析

正确答案

2，

解析

【解析】 （II）由（I）知椭圆的方程为

（i）设,由题意知，

因为,又， 即  ,

所以 ，即.

（ii）设，

将代入椭圆的方程，

可得，

由 ，可得

则有

所以

因为 直线与轴交点的坐标为，

所以 的面积

令,将代入椭圆的方程，

可得 ，

由，可得

由①②可知 ，

因此，故 ，

当且仅当时，即时取得最大值，

由（i）知，面积为，

所以 面积的最大值为.

考查方向

主要考查直线方程和椭圆方程联立，运用韦达定理，同时考查三角形的面积公式和二次函数的最值，属于中档题．

解题思路

（Ⅱ）求得椭圆E的方程，（i）设P（x0，y0），||=λ，求得Q的坐标，分别代入椭圆C，E的方程，化简整理，即可得到所求值；

（ii）设A（x1，y1），B（x2，y2），将直线y=kx+m代入椭圆E的方程，运用韦达定理，三角形的面积公式，将直线y=kx+m代入椭圆C的方程，由判别式大于0，可得t的范围，结合二次函数的最值，又△ABQ的面积为3S，即可得到所求的最大值．

易错点

直线与圆锥曲线的综合问题；椭圆的标准方程；曲线与方程．菁优网版权所有

1
题型：简答题
|
分值: 12分

设f（x）=sinxcosx﹣cos2（x+）．

16.求f（x）的单调区间；

17.在锐角△ABC中，角A，B，C的对边分别为a，b，c，若f（）=0，a=1，求△ABC面积的最大值．

第(1)小题正确答案及相关解析

正确答案

的单调递增区间是（）

单调递减区间是（）

解析

（Ⅰ）由题意

由，

可得，

由，

得，

所以的单调递增区间是（）

单调递减区间是（）

考查方向

本题主要考查了正弦函数的图象和性质

解题思路

（Ⅰ）由三角函数恒等变换化简解析式可得f（x），由，k∈Z可解得f（x）的单调递增区间，由,k∈Z可解得单调递减区间．

易错点

两角和与差的正弦函数的化简变换，正弦函数的单调性的整体变换

第(2)小题正确答案及相关解析

正确答案

解析

（II）

由题意A是锐角，所以 ，

由余弦定理：，

，

，且当时成立。

，

面积最大值为。

考查方向

考查余弦定理，基本不等式的应用，属于基本知识的考查．

解题思路

【解题思路】（Ⅱ）由，可得sinA，cosA，由余弦定理可得：，且当b=c时等号成立，从而得解．

易错点

余弦定理的变形，基本不等式的应用．

1
题型：简答题
|
分值: 12分

如图，在三棱台DEF﹣ABC中，AB=2DE，G，H分别为AC，BC的中点．

18.求证：BD∥平面FGH；

19.若CF⊥平面ABC，AB⊥BC，CF=DE，∠BAC=45°，求平面FGH与平面ACFD所成的角（锐角）的大小．

第(1)小题正确答案及相关解析

正确答案

连接，设，连接

在三棱台中，

，为的中点，

可得,

所以 四边形为平行四边形，

则 为的中点，

又 为的中点，

所以,

又平面    平面，

所以平面

解析

见答案

考查方向

考查棱台的定义，平行四边形的定义，线面平行的判定定理，面面平行的判定定理及其性质。

解题思路

（Ⅰ）根据AB=2DE便可得到BC=2EF，从而可以得出四边形EFHB为平行四边形，从而得到BE∥HF，便有BE∥平面FGH，再证明DE∥平面FGH，从而得到平面BDE∥平面FGH，从而BD∥平面FGH；

易错点

直线与平面平行的判定，构造线面平行或面面平行时辅助线或辅助面的作法．菁优网版权所有

第(2)小题正确答案及相关解析

正确答案

解析

（II）解法一：

设,则,

在三棱台中，

为的中点，

由,

可得 四边形为平行四边形，

因此,

又  平面，

所以 平面，

在中，由，，是中点，

所以 ,

因此 两两垂直，

以为坐标原点，建立如图所示的空间直角坐标系，

所以

可得

故，

设是平面的一个法向量，则

由  可得

可得 平面的一个法向量，

因为是平面的一个法向量，

所以

    所以平面与平面所成角（锐角）的大小为

考查方向

线面垂直的性质及线面垂直的判定定理，建立空间直角坐标系，利用空间向量求二面角的方法，平面法向量的概念及求法，向量垂直的充要条件，向量夹角余弦的坐标公式，平面和平面所成角的定义．

解题思路

（Ⅱ）连接HE，根据条件能够说明HC，HG，HE三直线两两垂直，从而分别以这三直线为x，y，z轴，建立空间直角坐标系，然后求出一些点的坐标．连接BG，可说明为平面ACFD的一条法向量，设平面FGH的法向量为，根据即可求出法向量，设平面FGH与平面ACFD所成的角为θ，根据cosθ=即可求出平面FGH与平面ACFD所成的角的大小．

易错点

二面角法向量的确定，二面角大小的观察。

1
题型：简答题
|
分值: 14分

设函数，其中。

26.讨论函数极值点的个数，并说明理由；

27.若>0，成立，求的取值范围。

第(1)小题正确答案及相关解析

正确答案

当时，函数有一个极值点；

当时，函数无极值点；

当时，函数有两个极值点。

解析

（Ⅰ）由题意知 函数的定义域为，

，

令，

（1）当时，，

此时，函数在单调递增，无极值点；

（2）当时，，

①当时，，,

，函数在单调递增，无极值点；

②当时，，

设方程的两根为，

因为，

所以，

由 ，可得，

所以 当时，，函数单调递增；

当时，，函数单调递减；

当时，，函数单调递增；

因此 函数有两个极值点。

（3）当时，，

由，可得，

当时，，函数单调递增；

当时，，函数单调递减；

所以函数有一个极值点。

综上所述：

当时，函数有一个极值点；

当时，函数无极值点；

当时，函数有两个极值点。

考查方向

本题考查了导数的运算法则、利用导数研究函数的单调性极值，考查了分类讨论思想方法、推理能力与计算能力。

解题思路

（I）函数f（x）=ln（x+1）+a（x2﹣x），其中a∈R，x∈（﹣1，+∞）．．令g（x）=2ax2+ax﹣a+1．对a与△分类讨论可得：（1）当a=0时，此时f′（x）＞0，即可得出函数的单调性与极值的情况．

（2）当a＞0时，△=a（9a﹣8）．①当时，△≤0，②当时，△＞0，即可得出函数的单调性与极值的情况．

（3）当a＜0时，△＞0．即可得出函数的单调性与极值的情况．

易错点

分类讨论函数取得极值的情况，注意函数单调性的制约作用。

第(2)小题正确答案及相关解析

正确答案

（Ⅱ）的取值范围是

解析

（II）由（I）知，

（1）当时，函数在上单调递增，

因为 ，

所以 时，，符合题意；

（2）当时，由，得，

所以 函数在上单调递增，

又，所以时，，符合题意；

（3）当时，由，可得，

所以时，函数单调递减；

因为，

所以时，，不合题意；

（4）当时，设，

因为时，

所以 在上单调递增。

因此 当时，，

即，

可得 ，

当时，，

此时 ，不合题意，

综上所述，的取值范围是

考查方向

本题函数恒成立问题，考查了分析问题与解决问题的能力，考查了分类讨论思想方法、推理能力与计算能力，属于难题．

解题思路

（II）由（I）可知：（1）当时，可得函数f（x）在（0，+∞）上单调性，即可判断出．

（2）当＜a≤1时，由g（0）≥0，可得x2≤0，函数f（x）在（0，+∞）上单调性，即可判断出．

（3）当1＜a时，由g（0）＜0，可得x2＞0，利用x∈（0，x2）时函数f（x）单调性，即可判断出；

（4）当a＜0时，设h（x）=x﹣ln（x+1），x∈（0，+∞），研究其单调性，即可判断出

易错点

利用导数研究函数恒成立问题，注意转化与化归思想的应用．菁优网版权所有

点击 “立即下载”

即可下载本试卷，含解析哦

知道啦