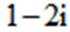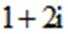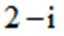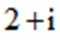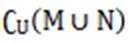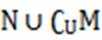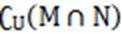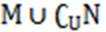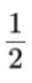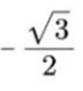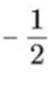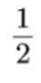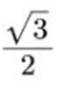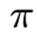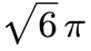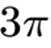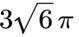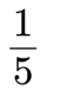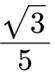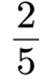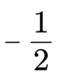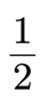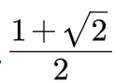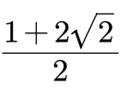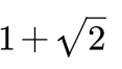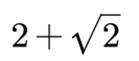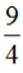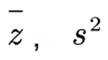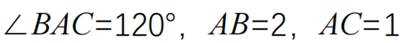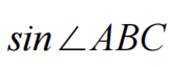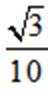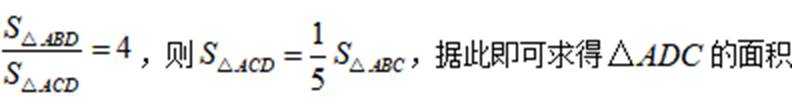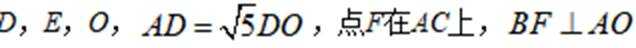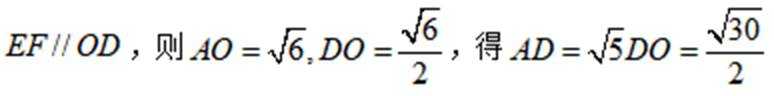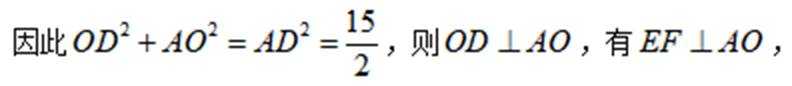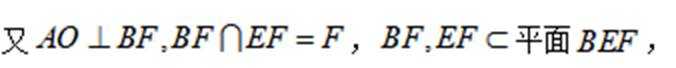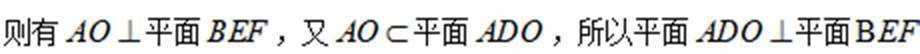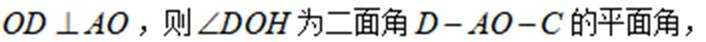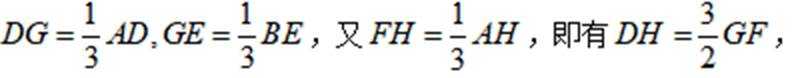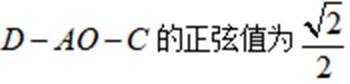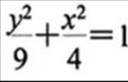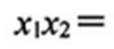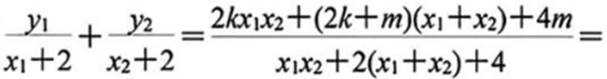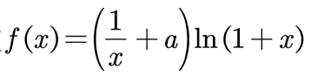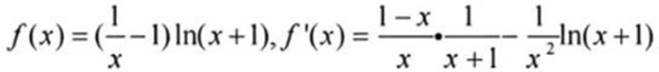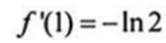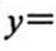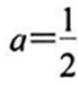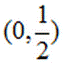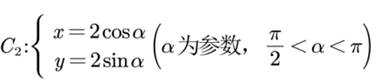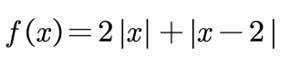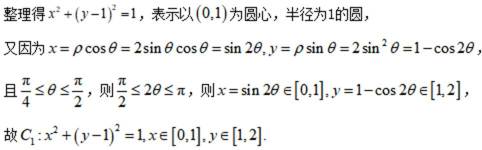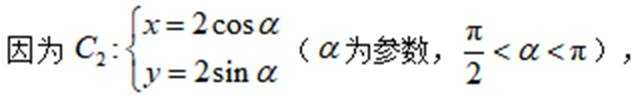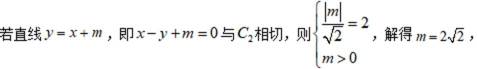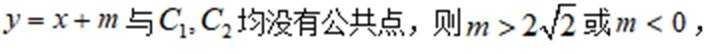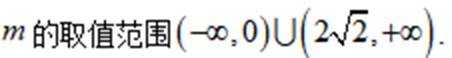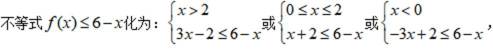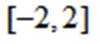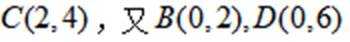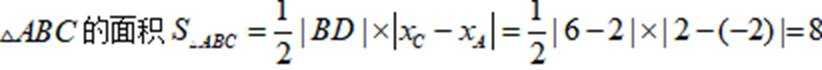- 真题试卷
- 模拟试卷
- 预测试卷
设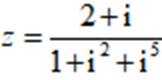
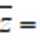
正确答案
设集合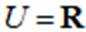
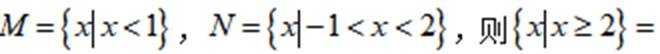
正确答案
如图,网格纸上绘制的一个零件的三视图,网格小正方形的边长为1,则该零件的表面积为( )
正确答案
已知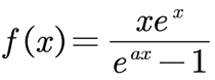
正确答案
设 O 为平面坐标系的坐标原点,在区域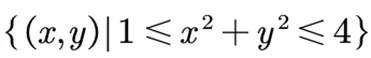
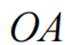
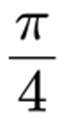
正确答案
已知函数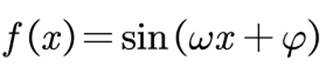
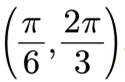

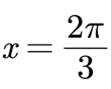
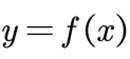
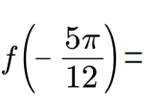
正确答案
甲乙两位同学从6种课外读物中各自选读2种,则这两人选读的课外读物中恰有1种相同的选法共有( )
正确答案
已知圆锥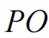
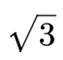
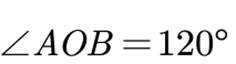
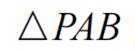
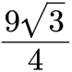
正确答案
已知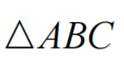
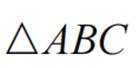
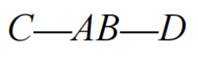
正确答案
已知等差数列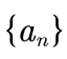
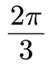
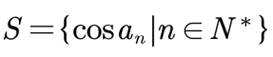
正确答案
设 A,B 为双曲线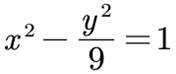
正确答案
已知

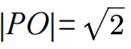
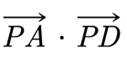
正确答案
已知点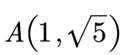
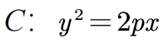
正确答案
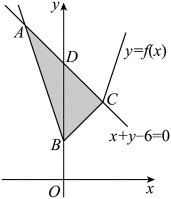
若 x,y 满足约束条件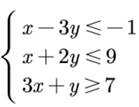
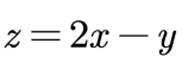
正确答案
8
已知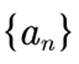
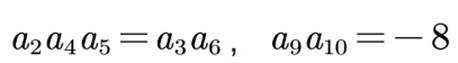
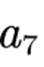
正确答案
-2
设 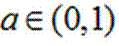
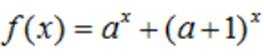
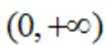
正确答案
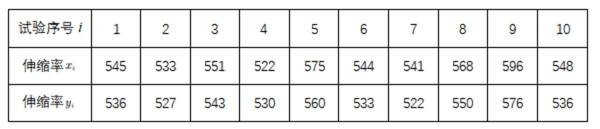
某厂为比较甲乙两种工艺对橡胶产品伸缩率的处理效应,进行 10 次配对试验, 每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测 量处理后的橡胶产品的伸缩率,甲乙两种工艺处理后的橡胶产品的伸缩率分别记为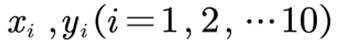
记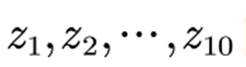
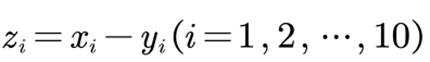
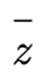
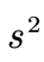
(1) 求
(2)判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高(如果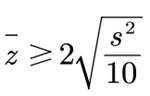
正确答案
(1) 11 ; 61 (2)有显著提高
18 .在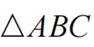
(1)求
(2)若 D 为 BC 上一点,且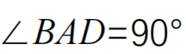
正确答案
(1)首先由余弦定理求得边长BC的值为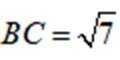
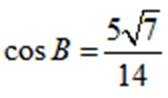
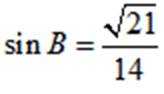
(2)
由题意得
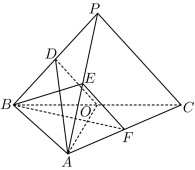
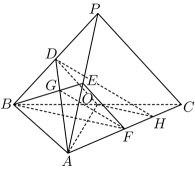
如图,在三棱锥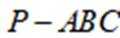
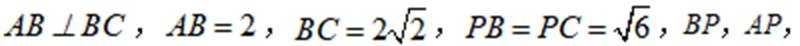
(1)证明: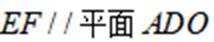
(2)证明: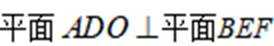
(3)求二面角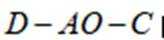
正确答案
(1)设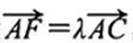
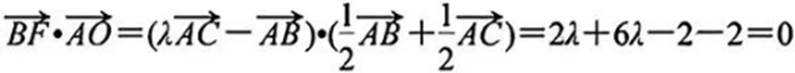
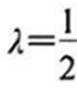
所以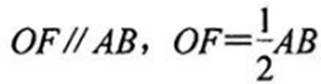
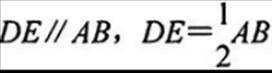
所以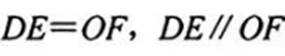
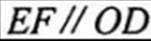

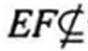
(2)由(1)可知
(3)过点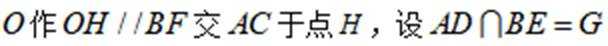
由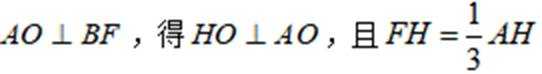
又由(2)知,
因为
即有
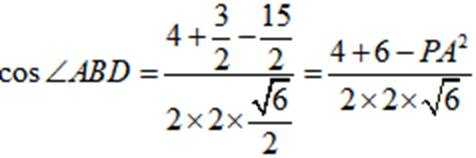

于是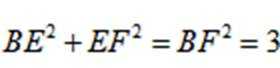
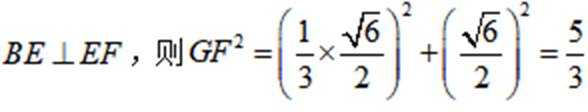
从而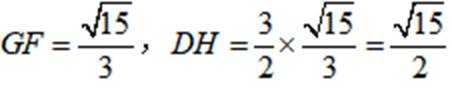
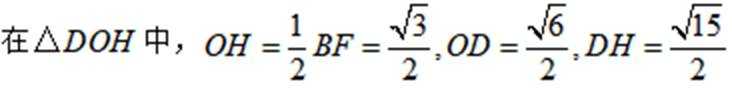
于是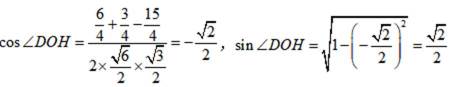
所以二面角
已知椭圆
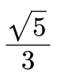
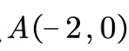
(1) 求 C 的方程
(2)2 点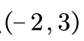
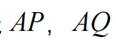
正确答案
(1) 由题意: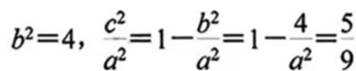
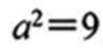
(2)设
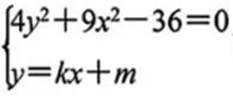
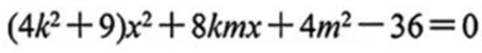
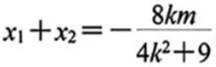
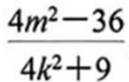
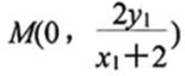
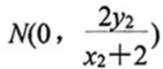
即线段MN的中点是定点(0,3)
已知函数
(1)当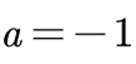
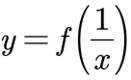
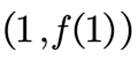
(2)是否存在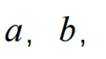
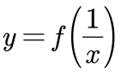
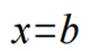
(3)若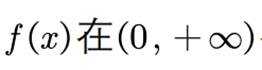
正确答案
(1)数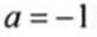
,
因为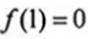
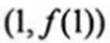
(2)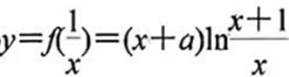
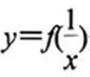
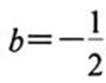
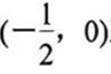
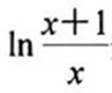
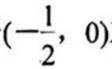
(3)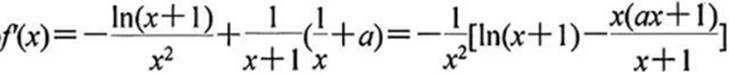
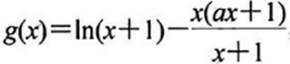
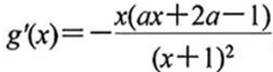
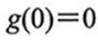
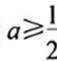
当a≤0时,g(x)>0,g(x)在区间(0,+∞)上递增,g(x)>0,f(x)<0,无极值点;
当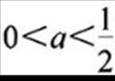
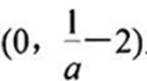
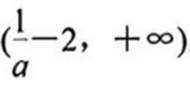
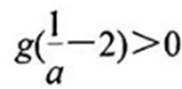
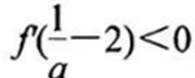
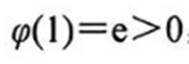
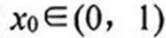
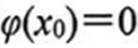
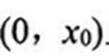
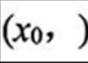


选做题
在直角坐标系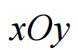
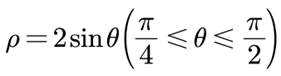
(1) 写出C 的直角坐标方程
(2)若直线 y=x+m 既与 c 没有公共点,也与c2没有公共点,求 m 的取值范围
已知
(1) 求不等式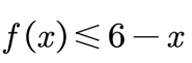
(2)在直角坐标系
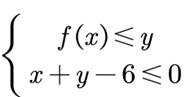
正确答案
(1)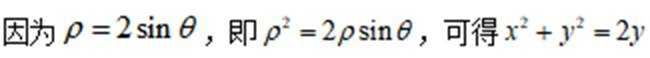
(2)
整理得
如图所示,若直线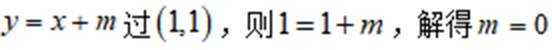
若直线
即实数
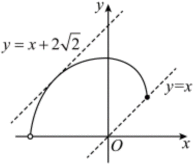
正确答案
(1)依题意,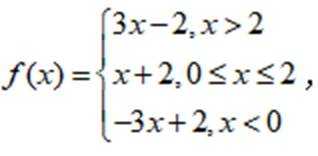
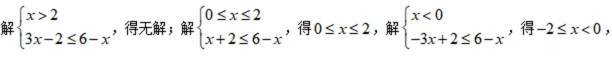

(2)作出不等式组
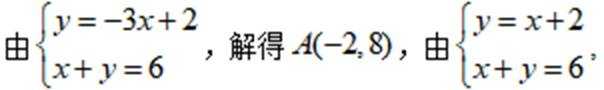
所以