- 真题试卷
- 模拟试卷
- 预测试卷
2、再计算
正确答案
2.已知i是虚数单位,则复数i(1+i)的共轭复数为( )
A.1+i
B.l﹣i
C.﹣l+i
D.﹣l﹣i
D
解析
由B中不等式变形得:x(x﹣2)≤0,
解得:0≤x≤2,即B=[0,2],∵A=[﹣1,1],∴A∩B=[0,1],故选:C.
考查方向
解题思路
先化简复数i(1+i)=i﹣1,再写出
易错点
本题易忽视最终所求为共轭复数。
12.设x,y满足约束条件
正确答案
9
解析
考查方向
解题思路
1、根据不等式组画画出约束条件表示的可行域,并画出函数的图像。
2、平移的图像与区域相交,从而找出最优解,并代入z=x+y得到Z的最大值。
易错点
1、本题易在根据不等式组画平面区域时出错。2、本题容易忽视“Z” 中的几何意义而出错。
知识点
13.在长为10cm的线段AB上任取一点C.现作一矩形,邻边长分别等于线段AC,CB的长,则该矩形面积不小于9cm2的概率为 .
正确答案
解析
设AC=x,则BC=10﹣x,
矩形的面积S=x(10﹣x)≥9,
∴x2﹣10x+9≤0,
∴1≤x≤9,
由几何概率的求解公式可得,矩形面积不小于9cm2的概率P= ,
故答案为: .
考查方向
解题思路
1、根据几何概型的概率公式,设AC=x,则BC=10﹣x,由矩形的面积S=x(10﹣x)≥9可求x的范围。
2、再利用几何概型的求解公式可求出概率。
易错点
本题易在由“矩形面积不小于9cm2”得到C所在范围时出错。
知识点
14.已知函数

正确答案
解析
考查方向
解题思路
1、先根据题意求得g(x)。
2、然后根据动直线x=t与函数y=f(x)和y=g(x)的图象分别交于M、N两点,可得|MN|=|f(x)﹣g(x)|,将两个函数的解析式代入化简为正弦型函数,再由正弦型函数的性质即可得到结论。
易错点
本题在理解“|MN|的最大值”为“|MN|=|f(x)﹣g(x)|的最大值”上易出错。
知识点
11.若(ax﹣l)6展开式中x3的系数为20,则a的值为 .
正确答案
-1
解析
(ax﹣l)6展开式的通项公式为 Tr+1=(﹣1)r•a6﹣r•x6﹣r,令6﹣r=3,求得r=3,
故展开式中x3的系数为﹣•a3=20,∴a=﹣1,
考查方向
解题思路
1、先写出通项再令x的幂指数等于3,求出r的值。
2、根据r找出含x3的项的系数即可。
易错点
1、本题易在书写通项时在“-”号上出错 。
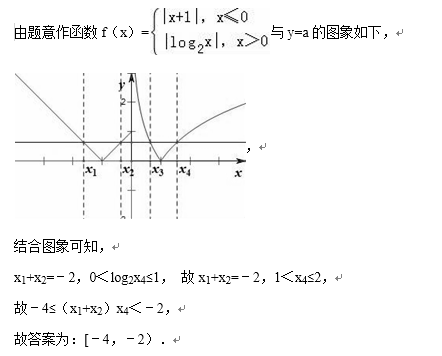
15.已知函数f(x)=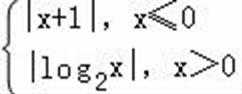
正确答案
[﹣4,﹣2)
解析
考查方向
解题思路
易错点
本题在用数形结合的思想把问题转化成图解过程中易出错。
知识点
3.某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了解该单位职工的心理状况,用分层抽样的方法从中抽取样本,若样本中的青年职工为7人,则样本容量为( )
正确答案
解析
设样本容量为n,则由题意得
解得n=15,故选:B
考查方向
解题思路
根据题意列出比例关系计算即可。
易错点
本题属实际应用问题,由于文字较长在从题目中提炼出数据时易出错。
知识点
7.在等比数列{an)中,al=1,公比|q|≠1,若am=a2a5a10,则m=( )
正确答案
解析
在等比数列{an}中,由al=1,am=a2a5a10,
得
又
故选A.
考查方向
解题思路
利用al=1化简am=a2a5a10为
易错点
本题只要能灵活al=1化简am=a2a5a10即可。
知识点
9.已知集合A﹣{1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )
正确答案
解析
A,如果输出b的值为792,则a=792,
I(a)=279,D(a)=972,b=D(a)﹣I(a)=972﹣279=693,不满足题意.
B,如果输出b的值为693,则a=693,
I(a)=369,D(a)=963,b=D(a)﹣I(a)=963﹣369=594,不满足题意.
C,如果输出b的值为594,则a=594,
I(a)=459,D(a)=954,b=D(a)﹣I(a)=954﹣459=495,不满足题意.
D,如果输出b的值为495,则a=495,
I(a)=459,D(a)=954,b=D(a)﹣I(a)=954﹣459=495,满足题意.
故选:D.
考查方向
解题思路
利用验证法判断每个选项,分条件不断赋值得到结论。
易错点
本题不易看出需由选项入手去完成而使问题复杂化。
知识点
1.已知集合A={x|﹣1≤x≤1),集合
正确答案
解析
约束条件
目标函数z=x+y经过可行域内的
目标函数取得最大值:9.
故答案为:9.
考查方向
易错点
本题是基础题,解题时只要认真审题,不会出错,属于送分题。
知识点
4.设函数f(x)=3x+bcosx,x∈R,则“b=0”是“函数f(x)为奇函数”的( )
正确答案
解析
若b=0,则f(x)=3x为奇函数,则充分性成立,
若函数f(x)为奇函数,则f(﹣x)=﹣3x+bcosx=﹣3x﹣bcosx,即b=﹣b,解得b=0,
即“b=0”是“函数f(x)为奇函数”充分条件和必要条件,
故选:C
考查方向
解题思路
等价转换“函数f(x)=3x+bcosx为奇函数”这句话为b=0再去判断。
易错点
本题易在“函数f(x)=3x+bcosx为奇函数”的化简上出错。
知识点
5.设 a=sin46°,b=cos46°,c=tan46°.则( )
正确答案
考查方向
易错点
1、本题在把题意转化成利用三角函数线去研究上易出错。(方法二)
知识点
6.如图,在△OAB中,点P在边AB上,且AP:PB=3:2.则
正确答案
考查方向
易错点
1、本题在AP:PB=3:2变换成
知识点
8.从某学习小组的5名男生和4名女生中任意选取3名学生进行视力检测,其中至少要选到男生与女生各一名,则不同的选取种数有( )
正确答案
考查方向
解题思路
1、利用计数原理构建数学模型。
易错点
本题在构建合适的数学模型完成计算上易出错。
知识点
10.已知
正确答案
考查方向
易错点
1、本题在根据题意转化为:
知识点
已知数列{an}的前n项和为Sn,且3Sn+2=4an(n∈N*).
18.求数列{an}的通项公式;
19.设bn=1og2an,数列{

正确答案
an=22n-1;
解析
试题分析:本题属于数列递推公式与数列裂项求和的应用问题,题目的难度适中。(1)求解时一定要灵活应用递推关系去发现an=4an﹣1;(2)在裂项相消求和时注意裂项求和方法的一些关键点。∵3Sn+2=4an,
∴当n=1时,3S1+2=4a1,
可得a1=2,
当n≥2时,4an﹣4an﹣1=3Sn+2﹣(3Sn﹣1+2),
化简得:an=4an﹣1,
∴数列{an}是以2为首项、4为公比的等比数列,
即an=2•4n﹣1=22n﹣1;
考查方向
解题思路
本题考查了数列的递推公式,数列求和中的裂项求和,不等式的解法及应用,解题步骤如下:1、通过在4an=3Sn+2中令n=1可得a1=2,当n≥2时,利用4an﹣4an﹣1=3Sn+2﹣(3Sn﹣1+2),可得an=4an﹣1,进而可得结论。2、由(1)得bn=1og222n-1=2n﹣1,
易错点
1、由递推关系3Sn+2=4an(n∈N*)得到an=4an﹣1时易忽视n=1而错解。
2、第二问在裂项求和过程中易出错。
正确答案
证明略。
解析
考查方向
易错点
1、由递推关系3Sn+2=4an(n∈N*)得到an=4an﹣1时易忽视n=1而错解。
已知向量


16.求函数f(x)的最小正周期;
17.当
正确答案
π;
解析
试题分析:本题属于三角公式与三角函数综合应用问题,题目的难度适中。(1)化简时一定要结合二倍角公式及辅助角公式灵活应用;(2)第二问属于给定区间求三角函数最值问题,要切实掌握这种方法的要领和步骤。
(I)f(x)=2cos2x+


∴f(x)的最小正周期T=
考查方向
解题思路
1、根据向量数量积公式利用二倍角公式与和角公式对f(x)进行化简。
2、根据x的范围得出
易错点
1、本题在第一问
2、本题第二问所涉及到给定区间求三角函数最值时易出现方法不熟而发生错误。
正确答案
[0,3]。
解析
∵x∈[




∴当2x+



∴函数f(x)的值域是[0,3].
考查方向
解题思路
1、根据向量数量积公式利用二倍角公式与和角公式对f(x)进行化简。
2、根据x的范围得出
易错点
1、本题在第一问
2、本题第二问所涉及到给定区间求三角函数最值时易出现方法不熟而发生错误。
如图,在平面四边形ABCD中,
20.求△ABC的面积S△ABC;
21.求CD的长.
正确答案
解析
试题分析:本题属于三角形中的正弦定理、余弦定理应用问题,题目的难度适中。(1)求解时一定要定位好研究那个三角形,利用面积公式计算面积。(2)在△BAD中由正弦定理得BD,再在△BAD中由余弦定理得CD。
由题意可得∠ACB=180°﹣(75°+30°+45°)=30°,
在△BAC中,由正弦定理可得BC=

sin∠ABC=sin105°=sin(60°+45°)=

∴△ABC的面积S△ABC=



考查方向
解题思路
本题考查了正弦定理、余弦定理应用,解题步骤如下:1、由题意在△BAC中由正弦定理可得BC,由和差角公式可得sin∠ABC,由三角形的面积公式可得。2、在△BAD中由正弦定理可得BD,由和差角公式可得cos75°,由余弦定理可得CD。
易错点
在角的计算上极易出错。
正确答案

解析
考查方向
易错点
第一问在角的计算上极易出错。
今年年初,我国多个地区发生了持续性大规模的雾霾天气,给我们的身体健康产生了巨大的威胁.私家车的尾气排放也是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
22.完成被调查人员的频率分布直方图;
23.若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为ξ,求随机变量ξ的分布列和数学期望.
正确答案
图略;
解析
试题分析:本题属常见的概率问题,在审题时一要会识图,二是要合理运用排列组合思想解决概率问题。其难度和其它概率问题一样难度适中,主要是题意的理解。
各组的频率分别是0.1,0.2,0.3,0.2,0.1,0.1.…
所以图中各组的纵坐标分别是0.01,0.02,0.03,0.02,0.01,0.01.…
∴被调查人员的频率分布直方图如右图:…
考查方向
解题思路
本题考查离散型随机变量的期望的计算,解题步骤如下:
1、由已知条件能求出图中各组的纵坐标,由此能完成被调查人员的频率分布直方图。2、由已知得ξ的所有可能取值为:0,1,2,3,分别求出p(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),由此能求出随机变量ξ的分布列和数学期望。
易错点
1、第一问在审题及结合频数分布表得出数据时易出错。
2、第二问排列组合思想的合理运用及期望的计算也是学生易错点。
正确答案

解析
考查方向
易错点
1、第一问在审题及结合频数分布表得出数据时易出错。
如图,有一块边长为1(百米)的正方形区域ABCD.在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45°(其中点P,Q分别在边BC,CD上),设BP=t.
24.用t表示出PQ的长度,并探求△CPQ的周长l是否为定值;
25.设探照灯照射在正方形ABCD内部区域的面积S(平方百米),求S的最大值.
正确答案

解析
考查方向
解题思路
本题考查了三角建模及正弦定理、余弦定理应用,解题步骤如下:
易错点
第一问由已知构造函数模型时易出错。
正确答案

解析
考查方向
易错点
1、第一问由已知构造函数模型时易出错。
已知函数f(x)=lnx,g(x)=ex,其中e是自然对数的底数,e=2.71828…
26.若函数

27.若x≥0,g(x)≥kf(x+1)+1恒成立,求实数k的取值范围
28.设直线l为函数f(x)的图象上一点,A(x0,f(x0))处的切线,证明:在区间(1,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切.
正确答案
函数φ(x)的单调递增区间为(0,1)和(1,+∞);
解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)利用导函数求出单调区间;
φ(x)=f(x)﹣

φ′(x)=
∵x>0且x≠1,∴φ'(x)>0,
∴函数φ(x)的单调递增区间为(0,1)和(1,+∞);
考查方向
解题思路
本题考查导数的性质及其应用,解题步骤如下:
1、求出原函数的导函数,确定导数恒大于0,从而可得求函数φ (x)的单调区间。
2、把g(x)≥kf(x+1)+1 (x≥0)恒成立,转化为kln(x+1)≤ex﹣1在x≥0时恒成立,然后分k≤0和k>0讨论,当k>0时,利用放缩法转化为kln(x+1)≤kx≤ex﹣1恒成立求解。
3、先求直线l为函数的图象上一点A(x0,f (x0))处的切线方程,再设直线l与曲线y=g(x)相切于点(

易错点
1、第二问在分类讨论
2、第三问证明在区间(1,+∞)上x0存在且唯一时极易出错。
正确答案
(﹣∞,e﹣1];
解析
解:由g(x)≥kf(x+1)+1 (x≥0)恒成立,
得ex≥kln(x+1)+1在x≥0时恒成立,
即kln(x+1)≤ex﹣1在x≥0时恒成立,
∵ex﹣1≥0,ln(x+1)≥0.
若k≤0,则kln(x+1)≤ex﹣1在x≥0时恒成立;
若k>0,由ln(x+1)≤x,得kln(x+1)≤kx,
由kx≤ex﹣1,知当x=0时,对于任意正实数k都成立,
当x>0时,不等式化为
令h(x)=

当x∈(0,1)时,h′(x)<0,当x∈(1,+∞)时,h′(x)>0,
∴h(x)有极小值也是最小值为h(1)=e﹣1.
∴当0<k≤e﹣1时,kln(x+1)≤kx≤ex﹣1恒成立.
综上,若x≥0,则使g(x)≥kf(x+1)+1恒成立的实数k的取值范围是(﹣∞,e﹣1];
考查方向
解题思路
本题考查导数的性质及其应用,解题步骤如下:
1、求出原函数的导函数,确定导数恒大于0,从而可得求函数φ (x)的单调区间。
2、把g(x)≥kf(x+1)+1 (x≥0)恒成立,转化为kln(x+1)≤ex﹣1在x≥0时恒成立,然后分k≤0和k>0讨论,当k>0时,利用放缩法转化为kln(x+1)≤kx≤ex﹣1恒成立求解。
3、先求直线l为函数的图象上一点A(x0,f (x0))处的切线方程,再设直线l与曲线y=g(x)相切于点(

易错点
1、第二问在分类讨论
2、第三问证明在区间(1,+∞)上x0存在且唯一时极易出错。
正确答案
证明略。
解析
证明:∵f′(x)=

∴切线l的方程为y﹣lnx0=
即y=
设直线l与曲线y=g(x)相切于点(
∵g′(x)=ex,∴
∴直线l方程又为y﹣


由①②得
∴
下面证明在区间(1,+∞)上x0存在且唯一.
由(1)可知,φ(x)=lnx﹣
又φ(e)=lne﹣


结合零点存在性定理,说明方程φ(x)=0必在区间(e,e2)上有唯一的根,这个根就是所求的唯一x0.
在区间(1,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切.
考查方向
解题思路
本题考查导数的性质及其应用,解题步骤如下:
1、求出原函数的导函数,确定导数恒大于0,从而可得求函数φ (x)的单调区间。
2、把g(x)≥kf(x+1)+1 (x≥0)恒成立,转化为kln(x+1)≤ex﹣1在x≥0时恒成立,然后分k≤0和k>0讨论,当k>0时,利用放缩法转化为kln(x+1)≤kx≤ex﹣1恒成立求解。
3、先求直线l为函数的图象上一点A(x0,f (x0))处的切线方程,再设直线l与曲线y=g(x)相切于点(

易错点
1、第二问在分类讨论
2、第三问证明在区间(1,+∞)上x0存在且唯一时极易出错。