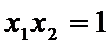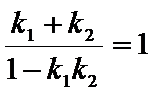- 真题试卷
- 模拟试卷
- 预测试卷
3.在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设全集U=R,集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.等差数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若向量









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.一组合体三视图如图,正视图中正方形边长为2,俯视图为正三角形及内切圆,则该组合体体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若椭圆或双曲线上存在点P,使得点P到两个焦点的距离之比为2:1,则称此椭圆或双曲线存在“F点”,下列曲线中存在“F点”的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.给出如下四个命题:
①四个非零实数




②设




③若

④若直线


其中错误命题个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在复平面内,复数
正确答案
二
解析
解析已在路上飞奔,马上就到!
知识点
10.在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若满足




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知点F是双曲线



正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
13.过抛物线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.将编号为1、2、3的三个小球,放入编号为1、2、3、4的四个盒子中,如果每个盒子中最多放一个球,那么不同的放球方法有____________种;如果4号盒子中至少放两个球,那么不同的放球方法有___________种.
正确答案
24,10
解析
解析已在路上飞奔,马上就到!
知识点
15.设函数
(1)求函数
(2)设A,B,C为



正确答案
(1)
=
所以函数


(2)




又因为在


所以
解析
解析已在路上飞奔,马上就到!
知识点
17.已知数列



(1)求证:数列
(2)求数列

正确答案
(1)∵

∵

∴
又
∴
∴数列


(2)由(1)得
∴

∴



将以上

∵
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数

(Ⅰ)若

(Ⅱ)若


正确答案
(Ⅰ)
当


因此曲线



(Ⅱ)
由(Ⅰ)知
即

此时

且
由

当


当


由以上讨论知,




解析
解析已在路上飞奔,马上就到!
知识点
16.已知三棱柱







(Ⅰ)证明:

(Ⅱ)试求线段MN与平面ABC的所成角的余弦值.
正确答案
(空间向量)
依条件可知




根据条件容易求出如下各点坐标:








(Ⅰ)因为

所以

又因为

且



(Ⅱ)
由





(逻辑推理)
(Ⅰ)如图
作出AC的中点D,连结DN,A1D.
∵D,N分别是AC,BC的中点
∴DN//AB且DN=
∵ABC-A1B1C1是三棱柱
∴AB//A1B1且AB=A1BA
又∵M是A1B1的中点
∴A1M=

∵DN//AB,AB//A1B1
∴DN//A1M
∴四边形A1DNM是平行四边形
∴MN//A1D
∵MN
A1D
∴MN//平面ACC1A1.
(Ⅱ)如图
作出AB的中点F
∵N,F分别是BC,AB的中点
∴NF//AC,NF=
又∵M是A1B1的中点
∴MF//AA1,MF= AA1=2
∵三棱柱
∴MF⊥NF
∴∠MFN就是所求的线面成角
∵
解析
解析已在路上飞奔,马上就到!
知识点
19.已知抛物线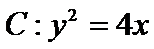
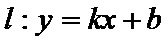
(Ⅰ)当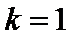
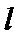
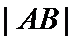
(Ⅱ)当直线OA,OB的倾斜角之和为45°时,求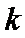
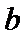
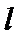
正确答案
(1)抛物线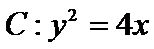
由已知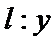
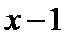
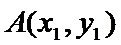
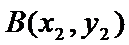
联立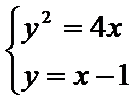
消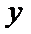
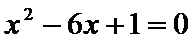
所以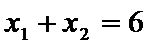
(2)联立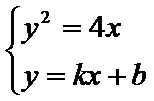
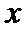
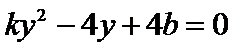
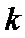
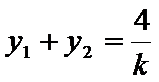
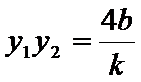
设直线OA,OB的倾斜角分别为α,β,斜率分别为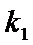
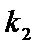
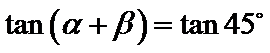
其中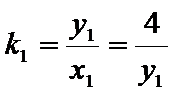
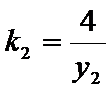
所以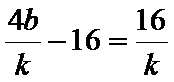
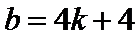
此时,使(*)式有解的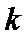
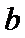
直线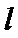
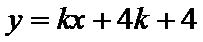
消去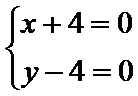
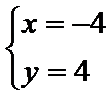
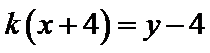
解析
解析已在路上飞奔,马上就到!
知识点
20.已知半椭圆













(1)若三角形
(2)若

(3)一条直线与果圆交于两点,两点的连线段称为果圆的弦.是否存在实数


正确答案
(1)∵F0(c,0)F1(0,

∴| F0F1 |=
于是



(2)由题意,得a+c>2b,即
∵(2b)2>b2+c2,∴a2-b2>(2b-a)2,得
又b2>c2=a2-b2,∴

(3)设“果圆”的方程为

记平行弦的斜率为k.
当k=0时,直线y=t(-b≤t≤b)与半椭圆



∴P、Q的中点M(x,y)满足
得
∵a<2b,∴
综上所述,当k=0时,“果圆”平行弦的中点轨迹总是落在某个椭圆
当k>0时,以k为斜率过B1的直线l与半椭圆
由此,在直线l右测,以k为斜率的平行弦的中点轨迹在直线
当k<0时,可类似讨论得到平行弦中点轨迹不都在某一椭圆上.
解析
解析已在路上飞奔,马上就到!