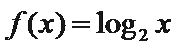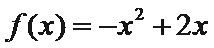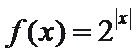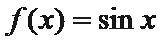- 真题试卷
- 模拟试卷
- 预测试卷
1.

正确答案
解析
奇数集合有三种表达方法
考查方向
解题思路
奇数集合有三种表达方法
易错点
奇数集合不熟
知识点
2.已知直线



正确答案
解析
设









考查方向
解题思路
直接证明,

易错点
容易出现分类讨论的疏漏错误
知识点
6.如果一个函数
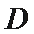

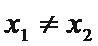
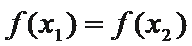
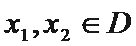
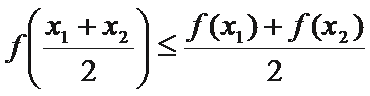
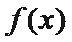
正确答案
解析
直接画图A、B、C、D四个选项的图像,逐一考查图像是否符合等式与不等式条件
考查方向
解题思路
直接画图A、B、C、D四个选项的图像,可以直接判断
易错点
对题中的等式与不等式理解不到位,导致无法判断
知识点
3.已知平面向量





正确答案
解析








考查方向
解题思路
可以由已知条件, 

易错点
数量积的运算律易出错
知识点
4.已知



正确答案
解析
函数图像的一个最高点与其相邻的一个最低点的距离为5,可求得水平距离为3,所以周期为6,则

考查方向
解题思路
先求周期为6, 再由公式求出
易错点
容易将题中的距离理解为水平距离,而错选C
知识点
5.已知异面直线

正确答案
解析
A. 符合异面直线定义,正确 ;B. 举出特例, 如图,正确;
C.正确,假设存在平面
考查方向
解题思路
根据题中的叙述条件画出图形, 结合定理.公理.性质进行论证.
易错点
对定理和性质掌握不准易出错
知识点
7.设双曲线C:







正确答案
解析
如图,过P作PH垂直x轴,根据PF平行渐近线,所以三角形POF为等腰三角形,OH=





考查方向
解题思路
画出双曲线的简图,结合双曲线渐近线的特点,得出a,b,c的数量关系,进而求出离心率
易错点
数形结合及数据推导容易出错
知识点
8.如图,在长方体








正确答案
解析
设直角三棱锥C-C’PQ的高为h, CQ=x,CP=y,根据直角三棱锥的性质可知,

















考查方向
解题思路
设CQ=x,CP=y, 根据直角三棱锥的性质



易错点
直角三棱锥的重要性质应用不熟
知识点
9.已知角



正确答案
-2,
解析
由三角函数定义,可知角











考查方向
解题思路
根据三角函数的定义,解出tan
易错点
定义理解不到位,公式应用错误
知识点
11.设等比数列




正确答案
32(

解析
根据题意依次算出等比数列的前四项,分别为











考查方向
解题思路
根据题意依次算出等比数列的前四项,分别为16,16,44,54,可判断出第二项不可能是16,所以该组数据中出错的是
易错点
本题易在“检验后发现其中恰好一个数算错了” 这句话理解上出错.
知识点
10.某几何体的三视图(单位:
几何体的表面积是 ▲ 

正确答案

解析
将三视图还原成直观图,如图所示,
S=3


考查方向
解题思路
将三视图还原成直观图,半个正方体直接计算表面积和体积
易错点
本题易在求表面积出错
知识点
12.过抛物线






正确答案
解析
设








考查方向
解题思路
先通过焦半径, 算出直线AB的倾斜角, 再利用数形结合的方法, 计算顶点到直线AB的距离
易错点
忽略AB是焦点弦, 找不到恰当的解题方法
知识点
13.在直角坐标系中,已知点







正确答案
4
解析
令a=0,则by



考查方向
解题思路
可令a=0 by



易错点
由可行域向不等式恒成立转化
知识点
14.若函数




正确答案
4,0,-16
解析
f(x-1)是偶函数,所以有f(x-1)= f(-x-1);所以有




考查方向
解题思路
根据题意,图像关于直线x=-1对称,所以将函数f(x)的图像向右平移一个单位,得到偶函数图像,再利用偶函数的性质,求出a与b,然后利用导数求函数的最小值
易错点
在对称性应用上易出错
知识点
15.已知点




正确答案
解析
设向量




所以|MA|:|MB|=|AC|:|CB|=2:1=k,


当
考查方向
解题思路
先化简已知条件

易错点
本题在由平面向量数量关系,转化到平面几何图形的相关数据
知识点
设△






已知
16.求
17.若

正确答案
解析
解:由


∴

考查方向
解题思路
可直接将题中的等式关系,用正弦定理将边的关系转成角的关系,再结合两角和公式,求出角A
易错点
问题容易在利用均值不等式放缩时出错
正确答案
解析
解:由

∴
∴
∴

又由题意知:
故:
考查方向
解题思路
可根据余弦定理, 得到b,c关系的等式, 再利用均值不等式进行合理缩放,可求出b+c取值范围
易错点
问题容易在利用均值不等式放缩时出错
如图,五面体





18.求证:直线

19.求二面角
正确答案
略
解析
解:在直角梯形

可得:


又∵


又


可得:
由①②可得:直线

考查方向
解题思路
先证出




易错点
在证明面面垂直时,没有严格按照定理的条件论证,重点是线面垂直,易在过程的严密性上扣分。
正确答案
解析
在直角梯形

可得:


又∵


又


可得:
由①②可得:直线

(Ⅱ)由(Ⅰ)知,建立如图空间直角坐标系,
由题意知各点坐标如下:

因此 
设平面

平面

由
可取
由
可取
于是
故二面角

考查方向
解题思路
(Ⅰ)先证出





易错点
(1).在证明面面垂直时,没有严格按照定理的条件论证,重点是线面垂直,易在过程的严密性上扣分。
(2).建立合理的坐标系,正确求点坐标
已知数列








24.比较


25.证明:

正确答案
解析
由

两式相减得:

又

∴

即:
考查方向
解题思路
先由通项及数列的前n项和的关系,求出通项,再求和,进而得出数列
易错点
在利用数列的前n项和与通项的关系时,易忽略对首项的验证
正确答案
略
解析
解:由(Ⅰ)知:

因此当

则
----------------------------------11分
又∵当

当且仅当
∴
∴

考查方向
解题思路
逐级对数列{






易错点
在构造数列放缩时,放缩不合理,导致出错
已知函数

20.若

21.若函数


正确答案



解析
解:
根据函数的图象可得, 


考查方向
解题思路
先将函数按照绝对值意义作分段函数,根据函数的图像,可求得单调区间
易错点
恰当选择a的分类标准,讨论区间
正确答案
解析
解:
(1).当





所以
在

(2).当



所以
综合(1)(2)得, 
考查方向
解题思路
结合函数的图象,对a进行分类
易错点
恰当选择a的分类标准,讨论区间
如图,已知椭圆



22.求椭圆
23. 若过点






正确答案
解析
解: 由已知可得, 
所求椭圆的方程为
考查方向
解题思路
列出a,b,c方程, 直接求椭圆的标准方程
易错点
解析几何易出现对于直线方程的分类讨论上的错误,其次就是直线与曲线联系以后,寻求变量之间的关系时,易出现转化、计算、代数整理的错误。
正确答案
直线

解析
解:设切线方程为


设两切线



由


同理可得:
所以




故直线

考查方向
解题思路
首先根据直线与圆相切得出
易错点
解析几何易出现对于直线方程的分类讨论上的错误,其次就是直线与曲线联系以后,寻求变量之间的关系时,易出现转化、计算、代数整理的错误。