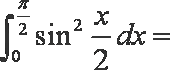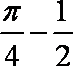- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合


正确答案
解析

知识点
3.下列函数中,其图象既是轴对称图形又在区间(0,+∞)上单调递增的是( )
正确答案
解析
对于A,函数y=
对于B,函数y=﹣x2+1的图象是轴对称图形,在区间(0,+∞)上是单调减函数,∴不满足题意;
对于C,函数y=2x的图象不是轴对称图形,∴不满足题意;
对于D,函数y=lg|x+1|的图象是关于直线x=﹣1对称的图形,且在区间(0,+∞)上是单调增函数,满足题意.
故选:D.
知识点
2.复数

正确答案
解析
∵复数z=1﹣i,∴





知识点
4.阅读如下程序框图,如果输出
正确答案
解析
根据算法的运算,第一次循环后



知识点
9.已知直线




正确答案
解析





知识点
6.下图是一容量为
正确答案
解析
根据中位数左右两侧的面积相等,也就是概率相等所以中位数为12,第一块的面积为
知识点
7.如图,网格纸上小正方形的边长为
正确答案
解析
由三视图可知,该多面体是一个四棱锥,且由一个顶点出发的三条侧棱两两垂直,长度都为4, ∴其体积为
知识点
11.若对


正确答案
解析
因为













知识点
8.在平面直角坐标系中,若


正确答案
解析
根据线性规划的方法可求得最优解为点

知识点
5.
正确答案
解析
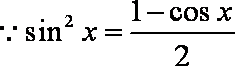
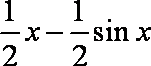
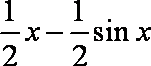
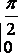
知识点
10.对定义在


(i) 对任意的

(ii) 当

则下列四个函数中不是
① 
③ 
正确答案
解析
在

对于①,
对于②,

对于③,




∴

对于④,

故选A.
知识点
12.已知直线






正确答案
解析
因为向量

知识点
14.正四面体



正确答案
解析
将四面体ABCD放置于正方体中,如图所示
可得正方体的外接球就是四面体ABCD的外接球,
∵正四面体ABCD的棱长为4,
∴正方体的棱长为
可得外接球半径R满足2R=
E为棱BC的中点,过E作其外接球的截面,当截面到球心O的距离最大时,
截面圆的面积达最小值,
此时球心O到截面的距离等于正方体棱长的一半,
可得截面圆的半径为r=
得到截面圆的面积最小值为S=
故答案为:4π
知识点
16.已知数列







正确答案

解析
∵



∴设

由上可知,数列



∴
即
令
则
②-①,得
∴
知识点
15.已知函数









正确答案
解析
由函数图像知:A=3,













知识点
13.
正确答案
解析
∵




知识点
20.已知函数
(1)求函数
(2)若函数
(3)若

正确答案
见解析。
解析
由已知函数


(1)函数
当




所以函数


(2)因f(x)在


所以当

又
故当


所以


(3)命题“若

“当

由(2),当


问题等价于:“当





则






故


(i)若





于是,

(ii)若





当





所以,


所以,

综上,得
知识点
19.已知椭圆


(1)求椭圆C的方程;
(2)设动直线


正确答案
(1)
(2)存在定点
解析
(1)由



在



联立①②得,
所以椭圆方程为
(2)设点





所以
由





因为以





则


知识点
17.工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人。现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别

(1)如果按甲最先,乙次之,丙最后的顺序派人,求任务能被完成的概率。若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(2)若按某指定顺序派人,这三个人各自能完成任务的概率依次为




(3)假定
正确答案
见解析。
解析
(1)无论以怎样的顺序派出人员,任务不能被完成的概率都是
(2)当依次派出的三个人各自完成任务的概率分别为

(3)(方法一)由(II)的结论知,当以甲最先、乙次之、丙最后的顺序派人时,
根据常理,优先派出完成任务概率大的人,可减少所需派出的人员数目的均值.
下面证明:对于


事实上,
即(*)成立.
(方法二)(i)可将(2)中所求的EX改写为


(ii)也可将(2)中所求的EX改写为


序综合(i)(ii)可知,当
知识点
21.如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD.
(1)求证:l是⊙O的切线;
(2)若⊙O的半径OA=5,AC=4,求CD的长.
正确答案
见解析。
解析
(1)证明:连接OP,因为AC⊥l,BD⊥l,
所以AC∥BD.
又OA=OB,PC=PD,
所以OP∥BD,从而OP⊥l.
因为P在⊙O上,所以l是⊙O的切线.
(2)
由上知OP=
所以BD=2OP﹣AC=6,
过点A作AE⊥BD,垂足为E,则BE=BD﹣AC=6﹣4=2,
在Rt△ABE中,AE=

∴CD=4
知识点
18.如图,在四棱锥


(1)求证:平面ABE⊥平面BEF;
(2)设


正确答案
见解析。
解析
(1)










(2) 

又


建系














知识点
22. 在直角坐标系


(1)求圆C的极坐标方程;
(2)直线



正确答案
见解析。
解析
(1)圆C的普通方程为
所以圆C的极坐标方程为
(2)设

设

所以