- 真题试卷
- 模拟试卷
- 预测试卷
2.已知复数z满足(1+2i)z=4+3i,则z=( )
正确答案
2-i
解析
解析已在路上飞奔,马上就到!
知识点
3.函数y=x2—2x (x∈[0,3]的值域是( )
正确答案
[-1,3]
解析
解析已在路上飞奔,马上就到!
知识点
4.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.在△ABC中,AB

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
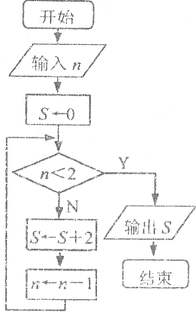
7.一个算法的流程图如图所示。若输入的n是100,则输出值S是( )
正确答案
198
解析
解析已在路上飞奔,马上就到!
知识点
8.已知集合A=(x,y)|x一2y一l=0},B={(x,y)|ax-by+1=0},其中a,b∈{1,2,3,4,5,6},则A∩B=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知

正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
6.已知直线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.对于函数
①
②
③
④
正确答案
①②④
解析
解析已在路上飞奔,马上就到!
知识点
13.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合M={x|0≤x-≤1},函数
正确答案
[0,1)
解析
解析已在路上飞奔,马上就到!
知识点
15.已知
(1)求函数
(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(1)若函数
(2)若p和q是方程

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知

(1)分别将两个圆的极坐标方程化为直角坐标方程;
(2)若两个圆的圆心距为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,

求证:
(1)PD//平面ABC;
(2)EC
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设
(1)求m的值,并确定函数
(2)判断函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.若存在实数k,b,使得函数





(1)函数


(2)函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知矩阵
(1)计算AB;
(2)若矩阵B把直线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24.某电视台的一个智力游戏节目中,有一道将四本由不同作者所著的外国名著A、B、C、D与它们的作者连线的题目,每本名著只能与一名作者连线,每名作者也只能与一本名著连线。每连对一个得3分,连错得一1分,一名观众随意连线,他的得分记作X。
(1)求该观众得分非负的概率;
(2)求X的分布列及数学期望。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.为了研究某种药物,用小白鼠进行试验,发现药物在血液内的浓度与时间的关系因使用方式的不同而不同。若使用注射方式给药,则在注射后的3小时内,药物在白鼠血液内的浓度




(1)若a=1,求3小时内,该小白鼠何时血液中药物的浓度最高,并求出最大值?
(2)若使小白鼠在用药后3小时内血液中的药物浓度不低于4,求正数a的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.如图所示,在直三棱

(1)证明:A1D⊥平面AB1C1;
(2)求二面角B—AB1—C1的余弦值;
正确答案
解析
解析已在路上飞奔,马上就到!