- 真题试卷
- 模拟试卷
- 预测试卷
6.已知数列的通项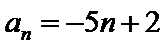
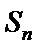
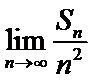
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 以

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若不等式

正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
2.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知平面向量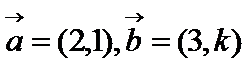

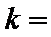
正确答案
-1或3
解析
解析已在路上飞奔,马上就到!
知识点
4.已知复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.袋中有大小相同的5个白球和3个黑球,从中任意摸出4个,求摸出2个或3个白球的概率_______________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若
正确答案
-189
解析
解析已在路上飞奔,马上就到!
知识点
12.将极坐标方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.定义在R上的函数




正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
15.设集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.若圆
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.对于使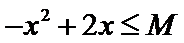
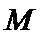
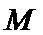
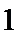
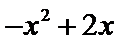
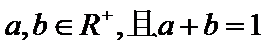
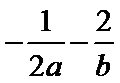
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知集合 
(1)若

(2)若

正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)求
(2)判断函数
(3)求函数的值域.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.已知数列



(1)求数列
(2)若函数

(3)设







正确答案
相加得:
所以
解析
解析已在路上飞奔,马上就到!
知识点
21.有一种变压器铁芯的截面呈如图所示的正十字形,为保证所需的磁通量,要求正十字形的面积为4
正确答案
设外接圆半径为R,AB =x(0<x<R),DG =y,则4R2=x2+y2 (1),
由已知条件有2xy-x2=4

代入(1)得4R2= x2 +
∴4R2=

当且仅当
代入(2)得y=1+
∴当 x=2 且y=1+
此时正十字形外接圆周长最短。
答:正十字形的长和宽分别为(1+
解析
解析已在路上飞奔,马上就到!
知识点
22.设斜率为











(1)求
(2)把上述椭圆








正确答案
(2)对于椭圆,
已知斜率为





点






则

(解一)设直线方程为
代入


得:

所以
即
(解二)设点
中点


又因为点
则
作差得
即
解析
解析已在路上飞奔,马上就到!