理科数学青岛市2012年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

2．已知R为全集，，，则是（）

A≤－1或

B<－1或

C<3或

D≤3或

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 5分

7．已知向量，的夹角为，且，则与的夹角等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

10．设，点为所表示的平面区域内任意一点，，为坐标原点，为的最小值，则的最大值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

1．若，其中，是虚数单位，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：单选题

分值: 5分

3．在面积为的的边上取一点，则的面积大于的概率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

分值: 5分

4．过点的直线与圆C：交于、两点，当最小时，直线的方程为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线的倾斜角与斜率

题型：单选题

分值: 5分

5．若函数的零点与的零点之差的绝对值不超过0．25，则可以是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

6．在上单调递减，那么实数的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

8．函数对任意的，都有，若函数，则的值是（）

B－5或3

C－2

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

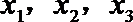
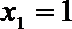
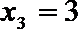
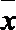
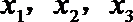
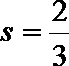
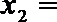
9．执行如下图所示的框图，输入，其中，，为的平均数，若输出的数，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

流程图的概念

题型：单选题

分值: 5分

12．在平面直角坐标系中，定义为点到点的一个点变换，已知P1（0，1），P2（x2，y2），…，（nN*）是经过点变换得到的一列点，设，数列的前n项和为，给出以下四个结论：

①；

②；

③；

④．

则正确结论的序号是（）

A①②④

B①②③

C②③④

D①③④

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：单选题

分值: 5分

11．已知抛物线的焦点与双曲线的一个焦点重合，则以此抛物线的焦点为圆心，以双曲线的离心率为半径的圆的方程是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

填空题本大题共5小题，每小题4分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 4分

14．若正三棱柱的底面边长为3，侧棱长为，则该棱柱的外接球的表面积为_______。

正确答案

36π

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：填空题

分值: 4分

16．给出以下命题：

①是成立的充分不必要条件。

②函数的最大值为2。

③正态分布曲线中，一定时，越小，曲线越“矮胖”，表明总体分布越分散。

④对于函数，若，则函数在内至多有一个零点。

其中正确命题的序号是___________（注：把你认为正确的命题的序号都填上）

正确答案

①②④

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：填空题

分值: 4分

13．已知函数，对任意的，，则的取值范围是_______。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

15．设是的展开式中的一次项的系数，则的值是_______。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：填空题

分值: 12分

17．在锐角中，分别是角所对的边．已知，且。

（1）求角的大小；

（2）记，求的值域。

正确答案

（1），

即，

，

（2），

锐角，

，

的值域为．

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

简答题（综合题）本大题共62分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

19．如图，四棱锥中，平面，，，，是的中点。

（1）求证：平面平面；

（2）求二面角平面角的正弦值。

正确答案

由于平面，，可建立以点A为坐标原点，

直线AB、AD、AE分别为轴的空间直角坐标系．

设，

则，，，，，

点是的中点，

即有

（1）证明：设平面的法向量为，

平面的法向量为，则有：

令，则

同理：

又

即平面平面

（2）由题意可知向量为平面的法向量，

设平面的法向量为

令，则

又

，

设二面角平面角为，则

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

分值: 12分

18．某学校举行定点投篮考试，规定每人最多投篮4次，一旦某次投篮命中，便可得到满分，不再继续以后的投篮，否则一直投到第4次为止．如果李明同学参加这次测试，设他每次定点投篮命中的概率依次为0．6，0．7，0．8，0．9。

（1）求他在本次测试中投篮次数的概率分布和数学期望；

（2）求他在本次测试中得到满分的概率。

正确答案

（1）随机变量1，2，3，4

P（1）=0．6

P（2）=0．40．7=0．28

P（3）=0．40．30．8=0．096

P（4）=0．40．30．2=0．024

解析

解析已在路上飞奔，马上就到！

知识点

随机事件的关系

题型：简答题

分值: 12分

20．已知为数列的前项和，且…

（1）求证：数列为等比数列；

（2）设，求数列的前项和。

正确答案

（1）证明：当时，

整理得

是以2为首项，以2为公比的等比数列

（2）解：由（1）得，

当为偶数时，

）

当为奇数时，可得

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：简答题

分值: 12分

21．已知函数。

（1）求；

（2）设，函数，若对于任意，总存在，使得成立，求的取值范围。

正确答案

（1），

，，

，

（2）由（1）知：，

，

，在为减函数，值域为

，

时，，在为减函数，

的值域为，

由题意知：只需，

又，

．

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 14分

22．如图，在直角坐标系中，O为坐标原点，直线轴于点，动点到直线的距离是它到点的距离的2倍。

（1）求点的轨迹方程；

（2）设点为点的轨迹与轴正半轴的交点，直线交点的轨迹于，两点（，与点不重合），且满足，动点满足，求直线的斜率的取值范围。

正确答案

（1）依题意知，点C（－4，0），

由得点D（－1，0）

设点M（），则：

整理得：

动点M的轨迹方程为

（2）当直线EF的斜率不存在时，由已知条件可知，O、P、K三点共线，直线PK的斜率为0．

当直线EF的斜率存在时，可设直线EF的方程为代入，整理

得

设

，K点坐标为（2，0）

，代入整理得

解得：

当时，

直线EF的方程为恒过点，与已知矛盾，舍去．

当时，

设，由知

直线KP的斜率为

当时，直线KP的斜率为0，符合题意

当时，

时取“=”）

或≤－时取“=”）

或

综合以上得直线KP斜率的取值范围是

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷