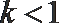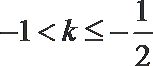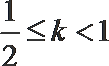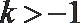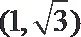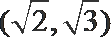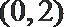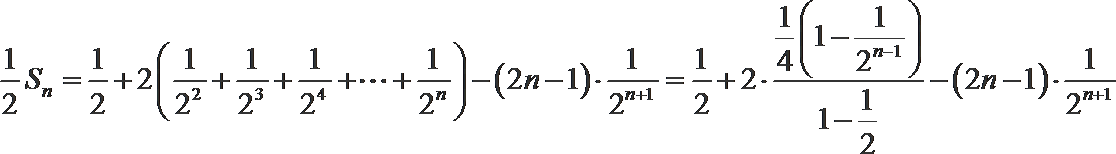- 真题试卷
- 模拟试卷
- 预测试卷
7. 已知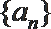
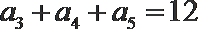
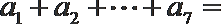
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 将一颗骰子掷两次,观察出现的点数并设第一次出现的点数为





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 如图所示是一个几何体的三视图,则该几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 设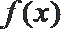
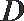
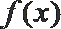
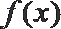
①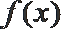
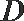
②存在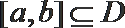
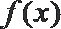
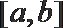
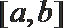
现已知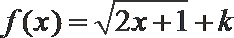

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 设锐角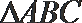
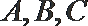
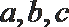
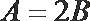
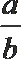
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 若复数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 如果执行右边的程序框图,且输入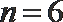
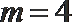
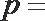
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 某班有男生30人,女生20人.现按分层抽样的方法抽取10人去参加座谈会,则女生应抽取人数为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 由曲线

正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
16. 给出下列命题:
①已知命题




②函数
③数列



④设


其中正确命题的序号是________.
正确答案
①②③④
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知数列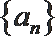


(1)求数列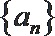
(2)设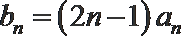
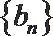
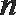
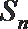
正确答案
解:(1)∵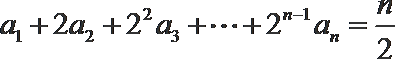
∴当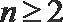
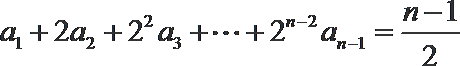
①-②得,

又∵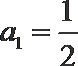
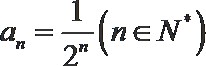
(2)由(1)知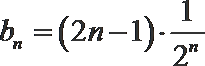
∴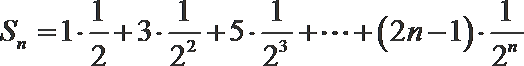
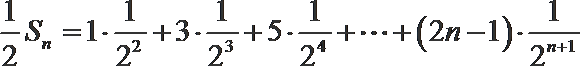
④-⑤得,
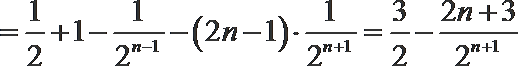
∴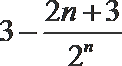
解析
解析已在路上飞奔,马上就到!
知识点
19. 有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
已知在全部105人中抽到随机抽取1人为优秀的概率为
(1)请完成上面的列联表;
(2)根据列联表的数据,若按
(3)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到6或10号的概率.
参考公式:
参考数据:
正确答案
解:(1)
(2)根据列联表中的数据,得到 
因此有95%的把握认为“成绩与班级有关系”.
(3)设“抽到6或10号”为事件A,先后两次抛掷一枚均匀的骰子,出现的点数为(x,y).
所有的基本事件有(1,1)、(1,2)、(1,3)、……、(6,6),共36个.
事件A包含的基本事件有:
(1,5)、(2,4)、(3,3)、(4,2)、
(5,1)(4,6)、(5,5)、(6、4),共8个

解析
解析已在路上飞奔,马上就到!
知识点
20. 如图,已知椭圆





(Ⅰ)设直线




(Ⅱ)是否存在常数


正确答案
(Ⅰ)设

因为点P在双曲线

因此

(Ⅱ)由于PF1的方程为

得
所以
同理可得

又
故
因此,存在

解析
解析已在路上飞奔,马上就到!
知识点
18. 如图,斜三棱柱




(1)求证:平面

(2)若二面角



正确答案
解:(1)取

则


(2)以






设

即
设面

面

解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(Ⅰ)求函数
(Ⅱ)记函数












正确答案
解:(Ⅰ)显然函数

由已知得,
(1)当




所以函数


(2)当





令

所以,函数



②当



③当




令

所以,函数



综上所述,地方有限, 略.
(Ⅱ)假设函数
设


且


曲线在点

依题意得:
化简可得: 


设



令

因为




所以在


综上所述,假设不成立.
所以,函数
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
22.选修4—1:几何证明选讲
如图,已知









(1)证明:
(2)若

23.选修4—4:坐标系与参数方程
在直角坐标系








(1)写出曲线

(2)求曲线

24.选修4—5:不等式选讲
若不等式



正确答案
22.
解:(1)∵



∵


(2)由(1)知



∵


由三角形内角和定理可知,
∵



∴
在Rt△


∴

23.
解:(1)由

由

所以,直线

(2)在

则点


所以当



24.
解:根据柯西不等式有







所以
解析
解析已在路上飞奔,马上就到!