- 真题试卷
- 模拟试卷
- 预测试卷
1.将函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设变量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 若角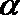
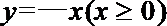
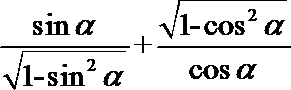
正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
6.用长为18m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,该长方体的最大体积是________
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知


(1) 
(2)
则
正确答案
1044
解析
解析已在路上飞奔,马上就到!
知识点
10. 当

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设函数











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知关于



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知非零向量a,b满足|a|=|a+b|=1,a与b夹角为120°,则向量b的模为( )
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
7.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知定义在



正确答案
(
解析
解析已在路上飞奔,马上就到!
知识点
9.在△ABC中,角A,B,C所对的边分别为a,b,c,已知a=1,A=60°,c=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数f(x)=2x2+m的图象与函数g(x)=ln|x|的图象有四个交点,则实数m的取值范围为( )
正确答案
(-∞,-
解析
解析已在路上飞奔,马上就到!
知识点
12. 在锐角


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 设



(1)若

(2)解关于x的不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 某广告公司为2010年上海世博会设计了一种霓虹灯,样式如图中实线部分所示。其上部分是以AB为直径的半圆,点O为圆心,下部分是以AB为斜边的等腰直角三角形,DE、DF是两根杆,其中AB=2 m,∠EOA=∠FOB=2x(0<x<)。现在弧EF、线段DE与线段DF上装彩灯,在弧AE、弧BF、线段AD与线段BD上装节能灯。若每种灯的“心悦效果”均与相应的线段或弧的长度成比,且彩灯的比例系数为2k,节能灯的比例系数为k(k>0),假定该霓虹灯整体的“心悦效果”y是所有灯“心悦效果”的和。
(1) 试将y表示为x的函数;
(2) 试确定当x取何值时,该霓虹灯整体的“心悦效果”最佳?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图

(1)求椭圆的标准方程;
(2)过椭圆的右顶点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列{an}的首项a1=a,Sn是数列{an}的前n项和,且满足:S=3n2an+S,an≠0,n≥2,n∈N*
(1)若数列{an}是等差数列,求a的值;
(2)确定a的取值集合M,使aM时,数列{an}是递增数列。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数


(1)求曲线
(2)若曲线

(3)试问:是否存在一条直线与曲线C同时切于两个不同点?如果存在,求出符合条件的所有直线方程;若不存在,说明理由。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点

(1)若平面ABC⊥平面BCC1B1,求证:AD⊥DC1;
(2)求证:A1B//平面ADC1 。
正确答案
解析
解析已在路上飞奔,马上就到!



















