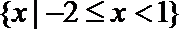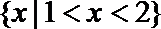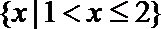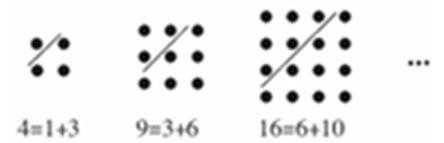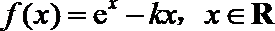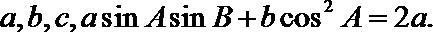- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知直线



①

②

③


④
其中正确命题的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.如图,





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设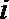
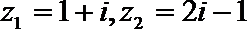

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.二项式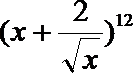
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
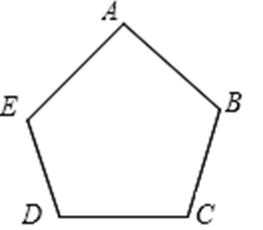
8.如图,正五边形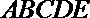
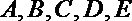
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.执行如图所示的程序框图,输出的
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.抛物线







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.某地区为某类人员免费提供财会和计算机培训,参加培训者可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有





正确答案
2.7
解析
解析已在路上飞奔,马上就到!
知识点
14.古希腊著名的毕达哥拉斯学派把1、3、6、10……这样的数称为“三角形数”,而把1、4、9、16……这样的数称为“正方形数”.如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式是( ).
①13=3+10; ②25=9+16; ③36=15+21; ④49=18+31; ⑤64=28+36
正确答案
③,⑤
解析
解析已在路上飞奔,马上就到!
知识点
17.对于函数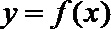
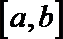
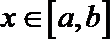
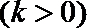
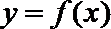
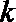
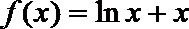
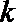
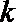
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.如图是一个组合几何体的三视图,则该几何体的体积是( ).
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列


(Ⅰ)若数列


(Ⅱ)若数列


正确答案
解:(I)由题意得

当

相减得


(Ⅱ)因为
则
令
相减得

故
解析
解析已在路上飞奔,马上就到!
知识点
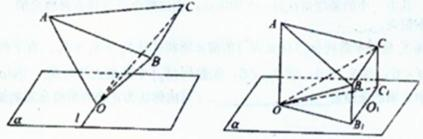
20.如图,一棱长为2的正四面体O—ABC的顶点O在平面α内,底面ABC平行于平面α,平面OBC与平面α的交线为
(1)当平面OBC绕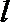
(2)在上述旋转过程中,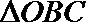
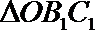
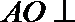
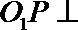
正确答案
(1)
(2)略
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(Ⅰ)若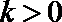
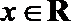
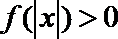
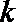
(Ⅱ)设函数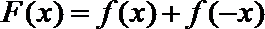
正确答案
②当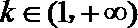
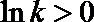
当
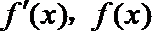
由此可得,在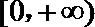
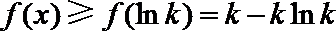
依题意,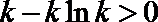

综合①,②得,实数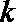
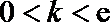
(Ⅱ)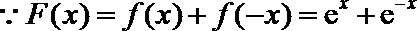
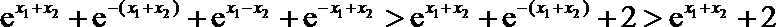
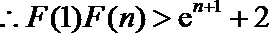
由此得,
故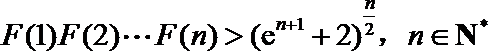
解析
解析已在路上飞奔,马上就到!
知识点
21.设椭圆C1:

(Ⅰ)求椭圆C1的方程;
(Ⅱ)设M(0,

正确答案
解:(Ⅰ)由题意可知B(0,-1),则A(0,-2),故b=2.
令y=0得

所以

(Ⅱ)设N(



代入椭圆方程整理得:




故

设点M到直线PQ的距离为d,则
所以,

当

综上可知,

解析
解析已在路上飞奔,马上就到!
知识点
18.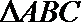
(1)求
(2)求A的取值范围。
正确答案
(1)2;
(2)
解析
解析已在路上飞奔,马上就到!