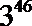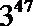- 真题试卷
- 模拟试卷
- 预测试卷
3.已知变量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若集合A=



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.程序框图(算法流程图)如图所示,其输出结果
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.定义在R上的奇函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.如图为一个几何体的三视图,主视图和左视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该几何体的表面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设



①若


②若




③若


④若





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.将数列
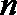
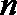
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知中心在原点的椭圆与双曲线有公共焦点,且左右焦点分别为






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若函数



正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
15.若存在实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.给出下列三个命题:
①函数

②若函数





③若奇函数



正确答案
②③
解析
解析已在路上飞奔,马上就到!
知识点
17.在




(1)求
(2)若


正确答案
解 (1)∵锐角B满足
∵

(2) ∵
∴
∴
∴
∴
∴
解析
解析已在路上飞奔,马上就到!
知识点
19.某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响. 已知某学生只选修甲的概率为



(1)记“函数



(2)求
正确答案
解:(1)设该学生选修甲、乙、丙的概率分别为

依题意得
若函数


当
∴事件

(2)依题意知
则
∴

解析
解析已在路上飞奔,马上就到!
知识点
18.已知数列







(1)求证:数列
(2)求数列
正确答案
解:(1)证明:



即
(2)由(1)知


解析
解析已在路上飞奔,马上就到!
知识点
20.如图,四棱锥









(1)点



(2)求证:无论点


(3)当


正确答案
.解:(1)当点E为BC的中点时,EF与平面PAC平行.
∵在△PBC中,E、F分别为BC、PB的中点,
∴EF∥PC.
又EF⊄平面PAC,而PC⊂平面PAC,
∴EF∥平面PAC.
(2)
证明:建立如图所示空间直角坐标系,则
(3)设平面PDE的法向量为
解析
解析已在路上飞奔,马上就到!
知识点
22.已知抛物线





(1)求证:


(2)设


正确答案
解:(1)设直线的方程为:
联立方程可得

设





而

即


(2)由


即得:

由(1)中②代入得

解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数



(1)求实数
(2)是否存在实数


正确答案
解:(1)



由①、②可得,
故实数a的取值范围是
(2)存在
由(1)可知




解析
解析已在路上飞奔,马上就到!