- 真题试卷
- 模拟试卷
- 预测试卷
2.若复数



正确答案
解析
设
考查方向
解题思路
研究复数问题一般将其设为


易错点
复数相等的条件
知识点
3.若线性方程组的增广矩阵为


正确答案
16
解析
由题意得:
考查方向
解题思路
线性方程组的增广矩阵是线性方程组另一种表示形式,明确其对应关系即可解决相应问题.即
易错点
矩阵与方程组的对应关系
知识点
5.抛物线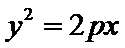
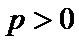
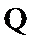

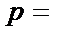
正确答案
2
解析
因为抛物线上动点到焦点的距离为动点到准线的距离,因此抛物线上动点到焦点的最短距离为顶点到准线的距离,即
考查方向
解题思路
标准方程中的参数p的几何意义是指焦点到准线的距离;p>0恰恰说明定义中的焦点F不在准线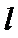
易错点
焦点与准线的关系
知识点
6.若圆锥的侧面积与过轴的截面面积之比为
正确答案
解析
由题意得:

考查方向
解题思路
掌握对应几何体的侧面积,轴截面面积计算方法.如 圆柱的侧面积 




易错点
几何体的空间结构
知识点
7.方程
正确答案
2
解析
设
考查方向
解题思路
对可化为a2x+b·ax+c=0或a2x+b·ax+c≥0(a2x+b·ax+c≤0)的指数方程或不等式,常借助换元法解决.求解与指对数有关的复合方程问题,首先要熟知指对数式的定义域、值域、单调性等相关性质,其次要明确复合的构成,涉及值域、单调区间、最值等问题时,都要借助“同增异减”这一性质分析判断,最终将问题归结为内层方程相关的问题加以解决.
易错点
准确换元
知识点
8.在报名的


正确答案
120
解析
由题意得,去掉选5名女教师情况即可:
考查方向
解题思路
涉及排列与组合问题,区分的关键是看选出的元素是否与顺序有关,排列问题与顺序有关,组合问题与顺序无关.“含”与“不含”的问题:“含”,则先将这些元素取出,再由另外元素补足;“不含”,则先将这些元素剔除,再从剩下的元素中去选取.通常用直接法分类复杂时,考虑逆向思维,用间接法处理.
易错点
本题方法较多需要灵活运用
知识点
9.已知点











正确答案
解析
由题意得:





考查方向
解题思路
(1)已知渐近线方程y=mx,若焦点位置不明确要分





易错点
双曲线焦点所在坐标轴
知识点
10.设



正确答案
4
解析
由题意得:






考查方向
解题思路
反函数与原函数的对应关系是解决问题的关键,一般有两个处理方法,一是从原函数出发求其反函数,再求函数最大值,本题求反函数教困难;二是利用反函数定义域对应原函数值域,反函数值域对应原函数定义域,反函数与原函数对偶区间上单调性一致,求出函数最大值.
易错点
求f(x)
知识点
1.设全集



正确答案
解析
因为
考查方向
解题思路
研究两集合的关系时,关键是将两集合的关系转化为元素间的关系,本题实质求满足属于集合A或不属于集合B的元素的集合.
易错点
研究集合问题,一定要抓住元素,看元素应满足的属性.
知识点
4.若正三棱柱的所有棱长均为


正确答案
4
解析
考查方向
解题思路
简单几何体的表面积和体积计算是高考的一个常见考点,解决这类问题,首先要熟练掌握各类简单几何体的表面积和体积计算公式,其次要掌握平几面积计算方法.柱的体积为



易错点
准确计算
知识点
11.在

正确答案
45
解析
因为



考查方向
解题思路
(1)求二项展开式中的指定项,一般是利用通项公式进行化简通项公式后,令字母的指数符合要求(求常数项时,指数为零;求有理项时,指数为整数等),解出项数r+1,代回通项公式即可.(2)对于三项式问题一般先变形化为二项式再解决.
易错点
三项式与二项式之间的转化处理
知识点
13.已知函数









正确答案
8
解析
因为




考查方向
解题思路
三角函数最值与绝对值的综合,可结合数形结合解决.极端位置的考虑方法是解决非常规题的一个行之有效的方法.
易错点
存在性问题的解法
知识点
12.赌博有陷阱.某种赌博每局的规则是:赌客先在标记有








正确答案
0.2
解析
赌金的分布列为
1
2
3
4
5
P
所以
奖金的分布列为
考查方向
解题思路
一般地,若离散型随机变量X的分布列为:
X
x1
x2
…
xi
…
xn
P
p1
p2
…
pi
…
pn
则称E(X)=x1p1+x2p2+…+xipi+…+xnpn为随机变量X的均值或数学期望,均值E(X)是一个实数,由x的分布列唯一确定,即X作为随机变量是可变的,而E(X)是不变的,它描述X值的取值平均状态.
易错点
期望求解的准确性
知识点
14.在锐角三角形













正确答案
解析
由题意得:


考查方向
解题思路
向量数量积的两种运算方法(1)当已知向量的模和夹角时,可利用定义法求解,即a·b=|a||b|cos<a,b>.(2)当已知向量的坐标时,可利用坐标法求解,即若a=(x1,y1),b=(x2,y2),则a·b=x1x2+y1y2.向量夹角与三角形内角的关系,可利用三角形解决;向量的模与三角形的边的关系,可利用面积解决.
易错点
准确的化简计算
知识点
17.记方程①:








正确答案
解析
当方程①有实根,且②无实根时,


考查方向
解题思路
根据方程根与判别式△之间的关系求出


易错点
数列性质与判别式的应用
知识点
15.设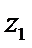
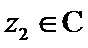
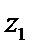
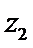
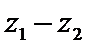
正确答案
解析
若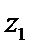
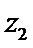
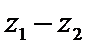
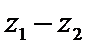
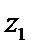
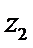
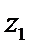
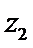
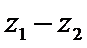
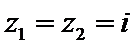
考查方向
解题思路
形如a+bi(a,b∈R)的数叫复数,其中a,b分别是它的实部和虚部.若b=0,则a+bi为实数;若b≠0,则a+bi为虚数;若a=0且b≠0,则a+bi为纯虚数.判断概念必须从其定义出发,不可想当然.
易错点
复数相等的条件
知识点
16.已知点






正确答案
解析



考查方向
解题思路
根据三角函数的定义,求出∠xOA的三角函数值,利用两角和差的正弦公式进行求解即可.
易错点
旋转前后的坐标问题
知识点
18.设




正确答案
解析
由题意得:因为





考查方向
解题思路
当n→+∞时,直线
易错点
数列数列极限思想的正确理解运用
知识点
19. 如图,在长方体






证明





正确答案
解析
试题分析: 利用长方体的几何关系建立直角坐标系.利用向量方法求空间角.
如图,以






因为

所以


即



设平面



又

故

取



故
因此直线


考查方向
解题思路
(1)设两条异面直线a,b的方向向量为a,b,其夹角为θ,则cos φ=|cos θ|=

易错点
线面夹角的证明;向量坐标运算的准确性
知识点
如图,
















20. 求

21. 已知警员的对讲机的有效通话距离是





正确答案
(1)

解析
试题分析: (1)由题意可得

(1)
记乙到


在

所以
考查方向
解题思路
解三角形时,有时可用正弦定理,有时也可用余弦定理,应注意用哪一个定理更方便、简捷.如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果遇到的式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.
易错点
实际问题数学模型的转化
正确答案
(2)

解析
试题分析:(2) 分段求出对应函数解析式,根据函数单调性求得最值即可.
(2)甲到达






当

当

所以
因为








考查方向
解题思路
分段求出各个段上的函数解析式及定义域.
易错点
分段函数单调性最值的求解
已知椭圆








22. 设






23. 设



正确答案
(1)略.
解析
试题分析:(1)依题意,直线l1的方程为
(1)证明:直线




所以
考查方向
解题思路
涉及弦长问题利用弦长公式解决,往往会更简单..
易错点
直线与椭圆的位置关系的计算问题
正确答案
(1)略(2)
解析
试题分析:(2)设直线l1的斜率为k,则直线l2的斜率为

(2)解:设



由

同理
由(1),
整理得
考查方向
解题思路
解决直线与椭圆的位置关系的相关问题,其常规思路是先把直线方程与椭圆方程联立,消元、化简,然后应用根与系数的关系建立方程,解决相关问题.
易错点
三角形面积公式的选用
已知数列



24. 若


25.设





26. 设







正确答案
(1)
解析
试题分析: (1)把bn=3n+5代入已知递推式可得an+1-an=6,由此得到{an}是等差数列,则an可求.
(1)解:由

所以


故


考查方向
解题思路
等差数列的四种判断方法:(1)定义法:an+1-an=d(d是常数)⇔{an}是等差数列;(2)等差中项法:2an+1=an+an+2(n∈N*)⇔{an}是等差数列;(3)通项公式:an=pn+q(p,q为常数)⇔{an}是等差数列;(4)前n项和公式:Sn=An2+Bn(A、B为常数)⇔{an}是等差数列.
易错点
等差数列性质的灵活运用
正确答案
(2)略.
解析
试题分析:(2)由


证明:(2)由

所以


因为



故

考查方向
解题思路
数列作为特殊的函数,其单调性的判断与研究也是特别的,只需研究相邻两项之间关系即可.
易错点
数列的单调性
正确答案
(3)
解析
试题分析:(3)由(2)可得

(3)因为

当

当

所以
因为


①当

②当




③当






综上,

考查方向
解题思路
数列作为特殊的函数,其单调性的判断与研究也是特别的,只需研究相邻两项之间关系即可.
易错点
分类讨论的不重不漏
对于定义域为












27. 验证

28. 设



29. 证明:“







正确答案
(1)略.
解析
试题分析:(1)根据余弦周期函数的定义,判断cosg(x+6π)是否等于cosg(x)即可.
证明:(1)易见

对任意

所以
即

考查方向
解题思路
新定义问题一般先考察对周期定义的理解
易错点
周期定义的理解运用
正确答案
(2)略
解析
试题分析:(2)根据f(x)的值域为R,便可得到存在x0,使得f(x0)=c,而根据f(x)在R上单调递增即可说明x0∈[a,b],从而完成证明;
(2)由于





若







考查方向
解题思路
新定义问题一般先考察对定义的理解,这时只需一一验证定义中各个条件即可.二是考查满足新定义的函数的简单应用,如在某些条件下,满足新定义的函数有某些新的性质,这也是在新环境下研究“旧”性质,此时需结合新函数的新性质,探究“旧”性质.三是考查综合分析能力,主要将新性质有机应用在“旧”性质,创造性证明更新的性质.
易错点
存在性问题与函数单调性最值的联系
正确答案
(3)略
解析
试题分析:(3)只需证明u0+T为方程cosf(x)=1在区间[T,2T]上的解得出u0为方程cosf(x)=1在[0,T]上的解,是否为方程的解,带入方程,使方程成立便是方程的解.证明对任意x∈[0,T],都有f(x+T)=f(x)+f(T),可讨论x=0,x=T,x∈(0,T)三种情况:x=0时是显然成立的;x=T时,可得出cosf(2T)=1,从而得到f(2T)=2k1π,k1∈Z,根据f(x)单调递增便能得到k1>2,然后根据f(x)的单调性及方程cosf(x)=1在[T,2T]和它在[0,T]上解的个数的情况说明k1=3,和k1≥5是不存在的,而k1=4时结论成立,这便说明x=T时结论成立;而对于x∈(0,T)时,通过考查cosf(x)=c的解得到f(x+T)=f(x)+f(T),综合以上的三种情况,最后得出结论即可.
(3)若








同理,若




以下证明最后一部分结论.
由(2)所证知存在






而





与之前类似地可以证明:





从而


故





对于


而

类似地,当




结论成立.
考查方向
解题思路
新定义问题一般先考察对定义的理解,这时只需一一验证定义中各个条件即可.二是考查满足新定义的函数的简单应用,如在某些条件下,满足新定义的函数有某些新的性质,这也是在新环境下研究“旧”性质,此时需结合新函数的新性质,探究“旧”性质.三是考查综合分析能力,主要将新性质有机应用在“旧”性质,创造性证明更新的性质.
易错点
周期定义的理解运用;存在性问题与函数单调性最值的联系;任意性问题成立的条件判断